Uma parede plana de espessura 0,6 m (L = 0,3 m) é feita de aço (k = 30 W/(m · K), ρ = 7900 kg/m³, c = 640 J/(kg · K)). Ela está inicialmente a uma temperatura uniforme e é, então, exposta ao ar em suas duas superfícies. Considere duas condições de convecção diferentes: convecção natural, caracterizada por h = 10 W/(m² · K), e convecção forçada, com h = 100 W/(m² · K). Você deve calcular a temperatura na superfície em três instantes diferentes: t = 2,5 min, 25 min e 250 min, para um total de seis diferentes casos.

(a) Para cada um desses seis casos, calcule a temperatura adimensional na superfície, , usando quatro métodos diferentes: solução exata, primeiro termo da solução em série, capacitância global e sólido semi-infinito. Apresente os seus resultados em uma tabela.

(b) Explique rapidamente as condições para as quais (i) a solução com o primeiro termo é uma boa aproximação para a solução exata, (ii) a solução da capacitância global é uma boa aproximação, (iii) a solução do sólido semi-infinito é uma boa aproximação.

Agora nós vamos calcular o número de Biot, para o caso de convecção natural, para poder encontrar os valores de na tabela B.3, então, temos:

E o número de Biot para convecção forçada será:

Nesse caso, vamos calcular para o caso de convecção natural. Então, os quatro primeiros termos de serão:

Agora, com esses valores, vamos encontrar os valores de , dados pela equação 5.39b vista nesse capítulo:

Então, substituindo os valores de , chegamos em:

Então, agora podemos calcular a expressão para descrita no passo 1, então, para t = 2,5 min, temos a seguinte tabela:

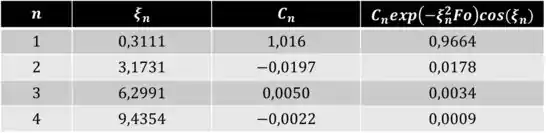
Então, como o quarto termo já é bem pequeno, não precisamos calcular o quinto, e essa é uma boa aproximação para a solução exata. Dessa forma então, temos:

Repetindo os cálculos para t = 25 min e t = 250 min, chegamos em:

Repetindo o procedimento para convecção forçada, com , nós chegamos nos seguintes resultados:

Agora, utilizando o método do primeiro termo da solução em série, que foi apresentada no passo 2, para convecção natural temos os seguintes resultados:

E, para conveccção forçada temos:

Beleza! Agora nós vamos utilizar o método da capacitância global, onde temos, da equação 5.6, que a temperatura adimensional é dada por:

Então, substituindo os valores conhecidos para convecção natural e para os diferentes intervalos de tempo, temos:

Repetindo os cálculos para convecção forçada, temos:

Agora vamos utilizar o método do sólido semi-infinito, então, da equação 5.63 vista nessa seção, temos:

Como estamos interessados na superfície, então iremos calcular em , dessa forma, a equação acima se torna:

No entanto, nosso é dado por:

Então, substituindo a expressão acima, temos:

Nós podemos escrever as expressões dentro de e de em função de Biot e de , nos quais os valores já são conhecidos, então, teremos:

Substituindo os valores conhecidos para os diferentes intervalos de tempo, temos:

Agora, repetindo os cálculos para convecção forçada, temos:

Agora, na letra (b), nós vamos analisar os resultados obtidos no passos anteriores. Então, para isso, vamos compilar todas as informações obtidas na tabela a seguir:

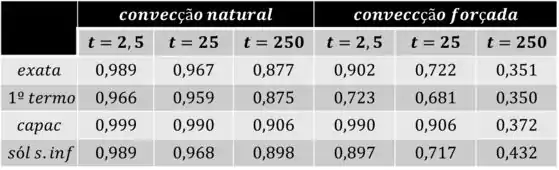
Então, para o primeiro caso (i), a solução com o primeiro termo é uma boa aproximação para a solução exata para t = 250 min, tanto para convecção natural quanto para convecção forçada.

Agora, para o caso (ii), a solução da capacitância global é uma boa aproximação para o caso onde temos convecção natural, para todos os intervalos de tempo.

E, para o caso (iii), a solução do sólido semi-infinito é uma boa aproximação para a solução exata para os intervalos de tempo de 2,5 e 25 minutos, em ambas as convecções.