Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 69

Um longo cilindro sólido, com diâmetro D = 25 mm, é formado por um núcleo isolante que é coberto por um revestimento metálico altamente polido e muito fino (t = 50 μm), com condutividade térmica de k   =   25 W m K . Corrente elétrica passa pelo aço inoxidável de uma

extremidade do cilindro para a outra, induzindo um aquecimento volumétrico uniforme no revestimento de q ˙ =   5   ×   10 6 W m 3 . Como ficará evidente no Capítulo 6, valores do coeficiente de transferência de calor entre a superfície e o ar nesta situação são especialmente não uniformes e, para as condições do escoamento do ar deste experimento, o coeficiente de

transferência de calor varia com o ângulo θ na forma h ( θ ) = 26 + 0,637 θ – 8,92 θ 2 , para 0 ≤ θ ≤ π 2 e h ( θ )   =   5 para π / 2   ≤   θ   ≤   π .

  1. Desprezando a condução na direção θ no aço inoxidável, represente graficamente a distribuição de temperaturas T ( θ ) para   0   ≤   θ   ≤   π e T ∞   =   25 ° C .
  2. Levando em conta a condução na direção θ no aço inoxidável, determine temperaturas no aço inoxidável em incrementos de Δ θ   = π 20 para 0   ≤   θ   ≤   π . Compare a distribuição de temperaturas com a da parte (a).

Sugestão: A distribuição de temperaturas é simétrica em relação à linha central horizontal do cilindro.

Passo 1

Animadíssimos?

Sei que estas questões são complicadas, mas nós vamos tentar simplificar ao máximo !!

Para a letra (a) nós vamos considerar um pequeno elemento, cujo comprimento do arco em um ângulo θ é D 2 ∆ θ para um metro de profundidade.

Não se esqueçam que aqui não temos condução de calor na direção θ , ok?

Quando nós aplicamos o nosso balanço de energia nós vemos que o calor que chega até o revestimento metálico sai por convecção, então:

q = h A T s - T ∞

Substituindo:

q ˙ A t = h A T ( θ ) - T ∞

q ˙ t = h ( θ ) T ( θ ) - T ∞

Isolando a temperatura:

T θ = T ∞ + q ˙ t h θ

Sabendo que:

q ˙ =   5   ×   10 6 W m 3

t =   50   μ m = 50 × 10 - 6 m

T ∞   =   25 ° C

h θ = 26 + 0,637 θ – 8,92 θ 2 ,       p a r a   0 ≤ θ ≤ π 2

h θ =   5 ,                                                                       p a r a π 2   ≤   θ   ≤   π

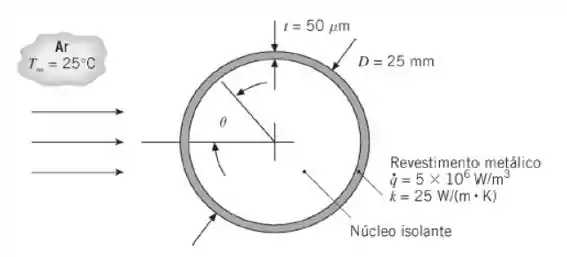
Então, para 0 ≤ θ ≤ π 2 :

T θ = 25 ° C + 5   ×   10 6 W m 3 50 × 10 - 9 m 26 + 0,637 θ – 8,92 θ 2

E para π 2   ≤   θ   ≤   π :

T θ = 25 ° C + 5   ×   10 6 W m 3 50 × 10 - 6 m 5 = 75 ° C

Na tabela:

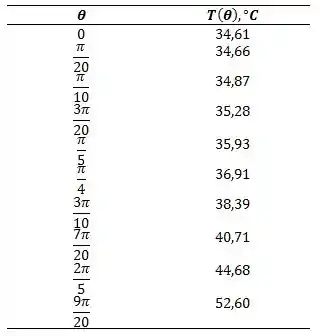
E colocando no gráfico:

Passo 2

Na letra (b) nós vamos levar em conta a condução na direção θ no aço inoxidável, e determinar as temperaturas no aço inoxidável em incrementos de Δ θ   = π 20 para 0   ≤   θ   ≤   π .

Como sabemos, o comprimento do arco é dado por:

∆ s = D 2 ∆ θ = 25 × 10 - 3 m 2 × π 20 = 1,96 × 10 - 3   m

Se o comprimento total é:

∆ s t = D 2 ∆ θ = 25 × 10 - 3 m 2 × π = 0,039   m

Então nós devemos dividir o arco em 20 partes, certo?

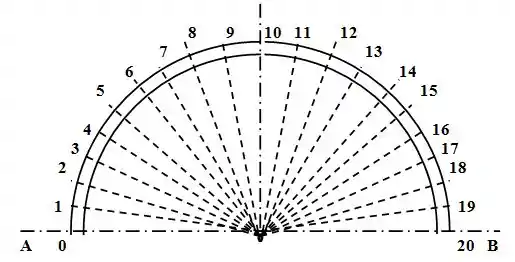
Agora nós precisamos do coeficiente convectivo para cada intervalo de ângulo, no caso de 0 ≤ θ ≤ π 2 , porque já sabemos que h θ =   5 ,       p a r a π 2   ≤   θ   ≤   π :

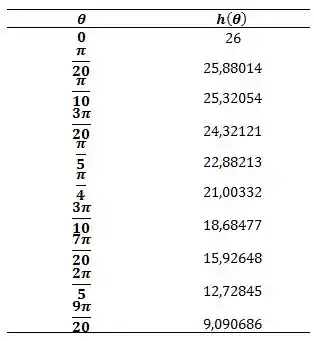
Para o Ponto 0:

k t ∆ s T 1 - T 0 + h ∆ s 2 T ∞ - T 0 + q ˙ ∆ s 2 t = 0

Substituindo nossos dados e não se esquecendo do coeficiente que varia para cada um:

25 W m K 50 × 10 - 6   m 1,96 × 10 - 3   m T 1 - T 0 + 26 W m 2 K 1,96 × 10 - 3   m 2 25 ° C - T 0 + 5 × 10 6 W m 3 1,96 × 10 - 3   m 2 50 × 10 - 6   m = 0

0,64 T 1 - 0,663 T 0 + 0,882 = 0

Para os Pontos 1 a 19:

k t ∆ s T m - 1 + T m + 1 - 2 T m + h ∆ s 25 ° C - T m + q ˙ ∆ s t = 0

Então:

0,64 T 0 + 0,64 T 2 - 1,326 T 1 + 1,758 = 0

0,64 T 1 + 0,64 T 3 - 1,325 T 2 + 1,7315 = 0

0,64 T 2 + 0,64 T 4 - 1,323 T 3 + 1,682 = 0

0,64 T 3 + 0,64 T 5 - 1,320 T 4 + 1,611 = 0

0,64 T 4 + 0,64 T 6 - 1,317 T 5 + 1,519 = 0

0,64 T 5 + 0,64 T 7 - 1,312 T 6 + 1,406 = 0

0,64 T 6 + 0,64 T 8 - 1,307 T 7 + 1,270 = 0

0,64 T 7 + 0,64 T 9 - 1,3 T 8 + 1,114 = 0

0,64 T 8 + 0,64 T 10 - 1,293 T 9 + 0,935 = 0

0,64 T 9 + 0,64 T 11 - 1,285 T 10 + 0,736 = 0

A partir deste ponto nós temos o coeficiente constante:

0,64 T 10 + 0,64 T 12 - 1,285 T 11 + 0,735 = 0

0,64 T 11 + 0,64 T 13 - 1,285 T 12 + 0,735 = 0

0,64 T 12 + 0,64 T 14 - 1,285 T 13 + 0,735 = 0

0,64 T 13 + 0,64 T 15 - 1,285 T 14 + 0,735 = 0

0,64 T 14 + 0,64 T 16 - 1,285 T 15 + 0,735 = 0

0,64 T 15 + 0,64 T 17 - 1,285 T 16 + 0,735 = 0

0,64 T 16 + 0,64 T 18 - 1,285 T 17 + 0,735 = 0

0,64 T 17 + 0,64 T 19 - 1,285 T 18 + 0,735 = 0

0,64 T 18 + 0,64 T 20 - 1,285 T 19 + 0,735 = 0

E para finalizar o Ponto 20:

k t ∆ s T 19 - T 20 + h ∆ s 2 T ∞ - T 20 + q ˙ ∆ s 2 t = 0

0,64 T 19 - 0,645 T 20 + 0,368 = 0

E resolvendo nossas reações simultaneamente:

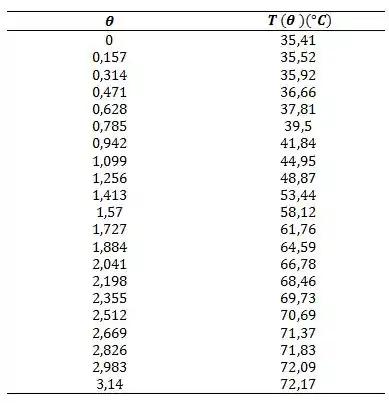
No gráfico:

E acabamos mais uma galerinhaa !!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em livros-texto sobre CFD [5, 23-27], frequentemente se substitui os lados esquerdos da equação (8.119b e c) pelas duas expressões seguintes, respectivamente: ∂ ∂ x u 2 + ∂ ∂ y ( v u ) ∂ ∂ x u v + ∂ ∂
A equação de Laplace em coordenadas polares planas, equação 8.11, é complicada pelo raio variável. Considere a malha de diferenças finitas na figura abaixo, com nós (i,j) igualmente espaçados de Δ θ e
Para escoamento incompressível laminar totalmente desenvolvido através de um duto retilíneo de seção não circular, como na seção 6.8, as equações de Navier-Stokes (4.38) se reduzem a ∂ 2 u ∂ y 2 + ∂ 2
Uma longa barra com seção transversal retangular, de 60m m × 90m m , tem condutividade térmica igual a 1W / m · K . Uma superfície está exposta a um processo de convecção com ar a 100°C e um coeficien
Um canal por onde passam gases quentes de exaustão apresenta uma seção transversal quadrada de 4 00m m de lado. As paredes são construídas com tijolos refratários com 20 0m m de espessura e condutivid