Considere um aquecedor elétrico delgado fixado a uma placa e isolado no outro lado. Inicialmente, o aquecedor e a placa se encontram à temperatura do ar ambiente, . Subitamente, a potência do aquecedor é ativada, fazendo-o liberar um fluxo térmico constante na superfície interna da placa.

(a) Esboce e identifique, em coordenadas , as distribuições de temperaturas: inicial, em regime estacionário e em dois tempos intermediários.
(b) Esboce o fluxo térmico na superfície externa como uma função do tempo.
Passo 1
Queremos nessa questão (a) esboçar a distribuição da temperatura em coordenadas, , e (b) esboçar o fluxo de calor na superfície externa, em função do tempo.
PRESSUPOSTOS:
(1) Condução unidimensional;
(2) Propriedades constantes;
(3) Perda desprezível de calor do aquecedor através do isolamento.
Passo 2
(a) Queremos plotar às distribuições de temperatura para quatro condições de tempo, incluindo a distribuição inicial, , e a distribuição em estado estacionário, . Podemos escrever a equação para a distribuição de temperatura no estado estacionário da seguinte maneira:
No início, temos que isso implica que , ou seja, par todo , a temperatura permanecera constante. Assim, podemos desenhar a distribuição de temperatura para o estágio inicial da seguinte maneira:

Passo 3
Agora, podemos desenhar a distribuição de temperatura para dois estágios intermediários da seguinte maneira:
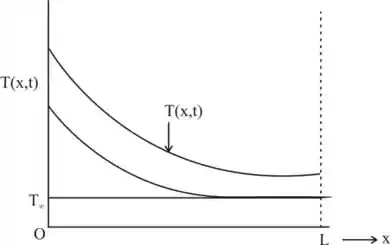
Isso é devido ao valor de não ter atingido o valor de estado estacionário que é .
Passo 4
Temos que o gradiente de temperatura quando for igual a zero será uma constante para , ou seja
pois o fluxo, , é uma constante. Assim, podemos desenhar a distribuição de temperatura para o estado estacionário com sendo uma função linear da seguinte maneira:
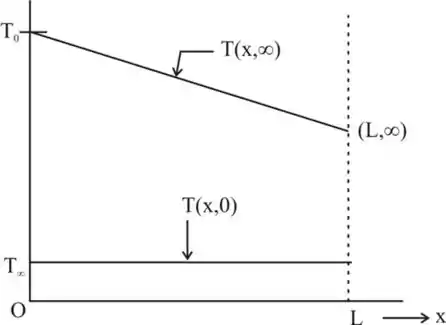
Passo 5
b) O fluxo de calor na superfície frontal, , é dado por
A partir da distribuição de temperatura, podemos construir o gráfico de fluxo de tempo e fluxo de calor da seguinte maneira:
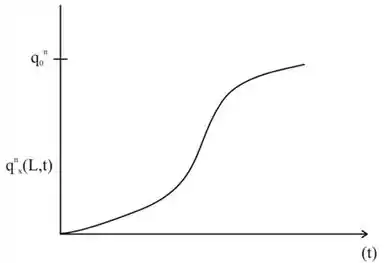
Resposta
Ei, a resposta está no passo a passo :)