Uma parede plana, com propriedades constantes e sem geração interna de calor, está inicialmente a uma temperatura uniforme . De repente, a superfície em é aquecida pelo contato com um fluido à temperatura , com um coeficiente de transferência de calor por convecção . No mesmo instante, o aquecedor elétrico é energizado, fornecendo um fluxo térmico constante em .

(a) Em coordenadas , esboce as distribuições de temperaturas para as seguintes condições: condição inicial , condição de regime estacionário , e dois tempos intermediários.
(b) Em coordenadas , esboce os fluxos térmicos correspondentes às quatro distribuições de temperaturas da parte (a).
(c) Em coordenadas , esboce os fluxos térmicos nas posições e . Ou seja, mostre qualitativamente como e variam com o tempo.
(d) Desenvolva uma expressão para a temperatura no regime estacionário da superfície do aquecedor, , em termos de e .
Passo 1
Vamos lá! primeiro vamos entender nosso problema, o problema diz que se trata de um sistema unidimensional, logo a troca de calor só ocorre em uma direção, vamos fazer nosso diagrama pra facilitar nossa vida.
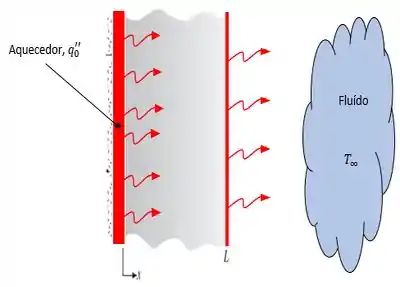
Origem e sentido do aquecimento da parede que depois perde calor para um fluido.
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a)
Tendo tudo isso em mente vamos a nossa letra (a), o gráfico de . Para isso vamos escrever nossa lei de Fourier (equação ).
Como nossa condução é unidimensional e não há geração de energia, temos:
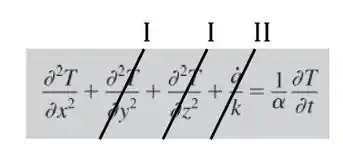
Assim nossa equação fica:
Como quanto nosso fluido aquecedor não aqueceu nossa superfície então a temperatura é , assim nossa equação fica:
Agora pra nossas condições de contorno, na superfície contraria ao aquecedor, não tem fluxo de calor, já que está isolada. Na outra superfície o fluxo de calor vai ser máximo, ou seja:
Assim nosso gráfico fica:
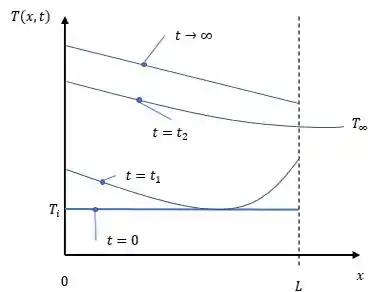
No instante nossa parede está roubando calor do ambiente e do aquecedor, nosso fluido está aquecendo a parede, após isso a parede já tem energia o suficiente para dissipa-la em forma de calor no fluido, assim o calor passa do aquecedor para a parede e pôr fim ao fluido.
Passo 3
(b) Bem nosso problema nos pede uma representação gráfica da distribuição do fluxo de temperatura ao longo da superfície, usar nossos cálculos da letra (a) nossa
Assim nosso gráfico fica assim.
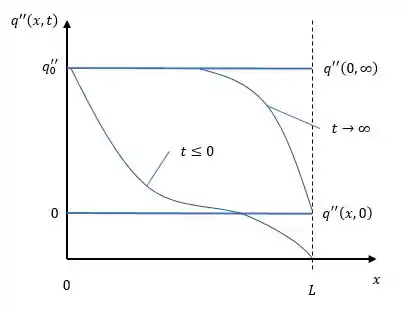
Esse intervalo negativo do fluxo é o resultado da nossa parede estar à uma temperatura menor que o fluido por isso o fluxo é negativo pois resulta do sentido do mesmo em sentido a parede.
Passo 4
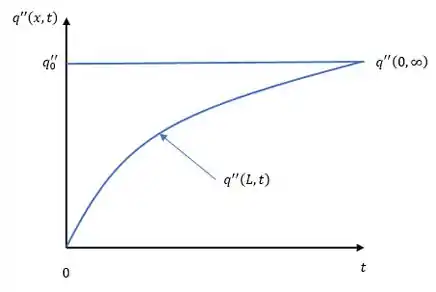
(c) Vamos lá! Nosso problema pede pra escrevermos o fluxo de calor em função do tempo. Temos que lembrar que no regime permanente nosso fluxo vai ser dado por:
Como com o passar do tempo a diferença de temperatura da superfície vai ser igual a temperatura do fluido que tá aquecendo a superfície.
Assim nosso gráfico fica assim.
Passo 5
(d) Estamos terminando! Para escrevermos nossa expressão pra temperatura no regime estacionário na superfície do aquecedor temos que fazer o balanço de fluxo, assim temos:
Combinando todas as equações temos:
Isso é tudo pessoal! \o/

Resposta
Ei, a resposta está no passo a passo :)