Uma longa haste cilíndrica, inicialmente a uma temperatura uniforme , é subitamente imersa em um grande reservatório de líquido a . Esboce a distribuição de temperaturas no interior da haste, , no instante inicial, no regime estacionário e em dois instantes intermediários. No mesmo gráfico, esboce cuidadosamente as distribuições de temperaturas que estariam presentes nos mesmos instantes em uma segunda haste, com as mesmas
dimensões da primeira. As massas específicas e os calores específicos das duas hastes são iguais, mas a condutividade térmica da segunda haste é muito grande. Qual haste irá se aproximar das condições de regime estacionário mais rápido? Escreva as condições de contorno apropriadas que seriam usadas em e em cada haste.
Passo 1
Vamos lá! primeiro vamos entender nosso problema, o problema diz que se trata de um sistema unidimensional sem geração de energia, logo a troca de calor só ocorre em uma direção que no caso apresentado é a radial, vamos fazer nosso diagrama pra facilitar nossa vida.
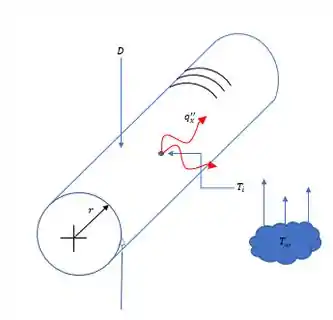
Sentido da dissipação de calor da haste cilíndrica.
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
Vamos lá, nossa questão pede a análise da dissipação de calor do cilindro, baseado nas nossas ultimas questões sabemos que nossa variação de temperatura tem aspecto.
Considerando que é relativamente alto temos.

Agora vamos lá, como a segunda haste tem um coeficiente de condução muito maior que a primeira tal que:
Agora pra segunda haste B no instante como é relativamente alta, mas em contraponto temos um coeficiente de convecção grande também, então assim que a barra entra em contato com nosso fluído o núcleo já começa a resfriar.
Já em um instante que seria o tempo do núcleo perder na barra , nossa barra já estará na temperatura do fluído pois o calor é dissipado muito rapidamente devido ao alto coeficiente convectivo
Para as condições de contorno baseado nas nossas informações temos nossas condições de contorno:
Isso é tudo pessoal! \o/

Resposta
Ei, a resposta está no passo a passo :)