20 – A partir do balanço de energia em um elemento de volume retangular, derive a equação de condução de calor unidimensional transiente para uma parede plana como condutividade térmica constante e sem geração de calor.
Passo 1
Para ajudar na visualização do problema:
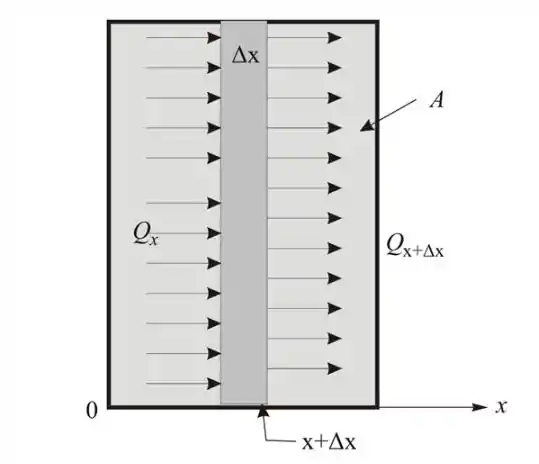
Passo 2
Premissas:
1) Unidimensional
2) Transitório
3) Condutividade térmica constante
4) Sem geração de calor
Vamos considerar um elemento fino de espessura em uma grande parede plana
A densidade da parede é ,
O calor específico é , e
A área da parede perpendicular à direcção de transferência de calor é .
Na ausência de geração de calor, um balanço de energia nesse elemento fino de espessura durante um pequeno intervalo de tempo pode ser expresso como
Onde:
Passo 3
Substituindo a relação (1), temos:
Ao consideramos o limite de e
Passo 4
A partir da definição da derivada e da lei de Fourier de condução de calor,
Observando que a área A de uma parede plana é constante, a equação de condução transiente unidimensional de calor em uma parede plana com condutividade térmica constante k se torna
Onde a propriedade é a difusividade térmica do material.
Portanto, a equação unidimensional de condução de calor para a parede plana é