Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 11.Exercício - Ex. 10

As partículas de um fluido movem-se no plano x y com trajetórias definidas por x = x 0 + t ; y = y 0 + t 2 .

  1. Obter a equação e desenhar a trajetória da partícula que, no instante t=0, encontra-se em P ( 0 ; 0 )
  2. Determinar a equação das linhas de corrente
  3. Obter a equação e desenhar a linha de corrente que passa por P ( 0 ; 0 ) , no instante t = 0,5 .
  4. O movimento é permanente ou variado?

Passo 1

Item A)

Primeiro vamos determinar as constantes x 0 e y 0 . Sabemos que quando t = 0 então x = 0 e y = 0 . Aplicamos isso nas equações abaixo:

x = x 0 + t ⇒ 0 = x 0 + 0 ⇒ x 0 = 0  

y = y 0 + t 2 ⇒ 0 = y 0 + 0 2 ⇒ y 0 = 0

Então:  

x = t

y = t 2

Hora, se x é igual a t , então podemos substituir na equação de y :

y = x 2

Agora vamos plotar isso com o Excel:

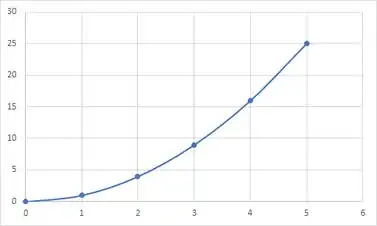
Passo 2

Item B)

Vamos determinar as velocidades:

v x = d x d t = d x 0 + t d t ⇒ v x = 1

v y = d y d t = d y 0 + t 2 d t ⇒ v y = 2 t

Utilizando as velocidades podemos calcular as linhas de corrente com a relação:

d x v x = d y d v y

d x 1 = d y 2 t

Integrando:

x = y 2 t + C

Passo 3

Item C)

x = y 2 t + C

Para t = 0,5 , x = 0 e y = 0

0 = 0 2 ⋅ 0,5 + C

C = 0

A equação é:

x = y 2 t

Para t = 0,5

x = y

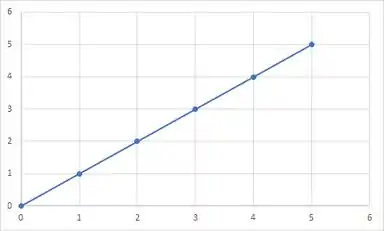
Passo 4

O regime é variado, já que a velocidade em um mesmo ponto muda ao longo do tempo!

Resposta

  1. y = x 2
  2. x = y 2 t + C
  3. x = y
  4. O regime é variado
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um líquido é drenado por um pequeno furo em um tanque, como mostra a Figura P4.60, de forma que o campo de velocidade é dado por v r ≈ 0 , v z ≈ 0 , v θ ≈ K R 2 / r , em que z = H é a profundidade da
Uma função corrente incompressível é definida por ψ x , y = U L 2 ( 3 x 2 y - y 3 ) em que UeL são constantes (positivas). Em que parte deste capítulo há um gráfico das linhas de corrente desse escoam
Investigue o potencial de velocidade ϕ = K x y ,K = c o n s t a n t e . Faça um esboço de linhas equipotenciais no plano xy completo, encontre quaisquer pontos de estagnação e faça um esboço aproximad
O Problema P4.38 pede para você encontrar a distribuição de pressão p ( r ) para a rotação de corpo sólido de um fluído, v θ = C r . Se z é “para cima, o resultado pode ser escrito da seguinte maneira
Investigue a função corrente ψ = K x 2 - y 2 ,K = c o n s t a n t e . Trace o gráfico de algumas linhas de corrente no plano xy completo, determine quaisquer pontos de estagnação e interprete o que o