Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 11.Exercício - Ex. 7
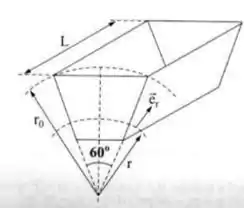
No funil da figura, escoa um líquido com o campo de velocidades
A vazão varia linearmente de até zero entre o instante inicia e o final, atingido após 2 min. Determinar:
- As componentes de velocidade
- A equação das trajetórias
- A aceleração
Passo 1
Item A)
Se a vazão varia linearmente de 1 à zero em 120 segundos, podemos presumir que sua função é
Aplicando a equação da continuidade:
Como a velocidade é normal à área:
A área de saída é proporcional ao comprimento L e ao arco.
Aplicando na integral com limites variando em 0 e 60 graus
A velocidade é:
Passo 2
Item B)
Vamos utilizar coordenadas cilíndricas. Nestas coordenadas, e .
Para a trajetória em
Integrando
Para ,
A equação do raio é:
Como: e
Passo 3
A velocidade é:
Utilizando a equação 11.4 podemos determinar a aceleração
Como e podemos reduzir para:
Resposta
- ;
Exercícios de Livros Relacionados
Para um escoamento no plano x y , a componente da velocidade em x é dada por u = A x 2 y 2 , em que A = 0,3m - 3 ⋅ s - 1 e x e y são medidos em metros. Determine uma possível componente y para escoame
As três componentes da velocidade em um campo de velocidade são dadas por u = A x + B y + C z , v = D x + E y + F z e w = G x + H y + J z . Determine a relação entre os coeficientes de A a J que é nec
Para um escoamento no plano x y , a componente x da velocidade é dada por u = A x ( y - B ) , em que A = 3,3m - 1 ⋅ s 1 , B = 1,8m e x e y são medidos em m . Encontre uma possível componente y para es
Para um escoamento no plano x y , a componente x da velocidade é dada por u = 3 x 2 y - y 3 . Encontre uma possível componente y para escoamento em regime permanente e incompressível. Ela também é vál
Quais dos seguintes conjuntos de equações representam possíveis casos de escoamento bidimensional incompressível?a) u = 2 x 2 + y 2 - x 2 y ; v = x 3 + x ( y 2 - 4 y ) b) u = 2 x y - x 2 y ; v = 2 x y