Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 60
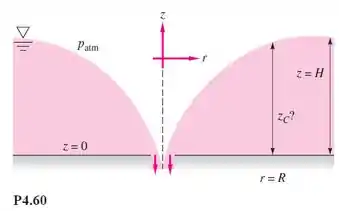
Um líquido é drenado por um pequeno furo em um tanque, como mostra a Figura P4.60, de forma que o campo de velocidade é dado por , em que é a profundidade da água distante do furo. Esse padrão de escoamento é rotacional ou irrotacional? Encontre a profundidade da água no raio
Passo 1
E vamos lá! Bora fazer mais uma!
Do apêndice D vamos usar a expressão de velocidade angular para verificar se o padrão é irrotacional! Ai, temos:
Assim, temos o padrão sendo irrotacional.
Passo 2
Tendo um fluxo incompressível, podemos usar Bernoulli, assim, considerando a pressão na superfície a pressão atm, teremos:
Tendo, e e incluindo na equação acima, teremos que:
Resposta
Irrotacional
Exercícios de Livros Relacionados
Um escoamento incompressível bidimensional é definido por u = K y x 2 + y 2 ; v = K x x 2 + y 2 em que K = constante. Esse escoamento é irrotacional? Em caso afirmativo, encontre seu potencial de velo
Um escoamento permanente, bidimensional, tem o seguinte potencial de velocidade em coordenadas polares: ϕ = C r c o s θ + K l n r em que C e K são constantes. Determine a função correnteψ ( r ,θ ) par
Em coordenadas esféricas polares, como na Figura P4.12, o escoamento é chamado de escoamento com simetria axial se v θ ≡ 0e∂ ∂ θ ≡ 0 , de forma que v r = v r r ,θev θ = v θ r , θ . Mostre que para ess
Um modelo CFD do escoamento incompressível permanente bidimensional imprimiu os valores da função corrente ψ (x, y), em m²/s, em cada um dos quatro cantos de uma pequena célula de 10 cm por 10 cm, com
Para a distribuição de velocidade do Problema P4.4, determine se existe uma função corrente e, se existir, encontre uma expressão para ψ ( x , y ) e faça o esboço da linha de corrente que passa pelo p