Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 197

Um pequeno regador de gramados é mostrado (Problema 4.196). Ele opera com uma pressão manométrica na entrada de 140   k P a . A vazão total em volume de água através do regador é de 4,0   L / m i n . Cada jato descarrega água a 17   m / s (em relação ao braço do regador) com uma inclinação de 30 ° para cima em relação ao plano horizontal. O regador gira em torno de um eixo vertical (pivô). O atrito no pivô causa um torque de oposição à rotação de 0,18   N ⋅ m . Determine a velocidade de rotação em regime permanente do regador e a área aproximada coberta pelos jatos de água.

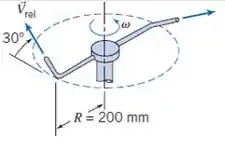
Passo 1

Equação:

r × F s + ∫ V C r × g ρ d ∀ + T e i x o - ∫ V C r × 2 ω × V + ω × ω × r + ω × r ρ d ∀ = ∂ ∂ t ∫ V C r × V ρ d ∀ + ∫ S C r × V   ρ V d A

Considerações Iniciais:

  1. Fluxo Constante;
  2. Escoamento Estacionário;
  3. Cancelamento do torque no corpo;
  4. F S = 0 .

Passo 2

Realizando as considerações:

T e i x o = ∫ S C r × V   ρ V d A

Temos:

T e i x o = - T f k ^

- T f k ^ = r × V m - ρ Q + 2 r × V j a t o ρ Q 2

Sendo:

r × V m = 0 ;

r = R   î r ;

V = R ω - V r e l cos ⁡ α î θ + V r e l   s e n   α   î z .

Temos:

r × V = R   î r × R ω - V r e l cos ⁡ α î θ + V r e l   s e n   α   î z

Sendo:

î r × î θ = î z ;

î r × î z = - î θ ;

Temos:

r × V = R { R ω - V r e l cos ⁡ α - î z + s e n   α   - î θ }

Então:

r × V z = R R ω - V r e l cos ⁡ α

Desse modo:

- T f = 2 R R ω - V r e l cos ⁡ α ⋅ ρ Q 2

T f = R ρ Q R ω - V r e l cos ⁡ α

Isolando ω :

ω = V r e l cos ⁡ α R - T f ρ Q R 2

Passo 3

Sendo:

T f = 0,18   N ⋅ m ;

R = 200   m m = 0,2   m ;

V r e l = 17   m / s ;

ρ = 1000   k g / m 3 ;

Q = 4   L / m i n = 6,67 x 10 - 5   m 3 / s ;

θ = 30 ° ;

Temos:

ω = 17 ⋅ cos ⁡ 30 ° 0,2 - 0,18 1000 ⋅ 6,67 x 10 - 5 ⋅ 0,2 2 = 6,15   r a d / s

Passo 4

Tratando o jato saindo de cada bico se movendo sem resistência do ar.

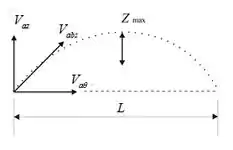
Para cada partícula:

d V a z d t = - g

V a z = - g t

t = - V a z g

O tempo de voo é dado por:

L = 2 t V θ

L = 2 ⋅ - V a z g ⋅ R ω - V r e l cos ⁡ α = 2 V a z V r e l cos ⁡ α - R ω g

Sendo V a z = V r e l s e n   θ

L = 2 ⋅ V r e l s e n   θ ⋅ V r e l cos ⁡ α - R ω g

Passo 5

Sendo:

R = 200   m m = 0,2   m ;

V r e l = 17   m / s ;

θ = 30 ° ;

ω = 6,15   r a d / s ;

g = 9,8   m / s 2 .

Temos:

L = 2 ⋅ 17 ⋅ s e n   30 ° ⋅ 17 ⋅ cos ⁡ 30 ° - 0,2 ⋅ 6,15 9,8 = 23,4   m

Agora, calcularemos a distância percorrida pelo jato:

L j a t o = R 2 + L 2 = 0,2 2 + 23,4 2 = 23,4   m

Calculando a área coberta pelos jatos:

A = π R 2 = π ⋅ 23,4 2 = 1720   m 2

Resposta

ω = 6,15   r a d / s

A = 1720   m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um aerofólio com um ângulo de ataque a, como na Figura P 3.150 , proporciona sustentação pelo efeito Bernoulli, porque a superfície inferior retarda o escoamento (alta pressão) e a superfície superior
Água flui por um bocal circular, sai para o ar na forma de um jato e colide com uma placa, como mostra a Figura P 3.151 . A força necessária para manter a placa estacionária é 70N . Admitindo escoamen
O escoamento de ar debaixo de um disco de hóquei de mesa é muito complexo, especialmente porque os jatos da mesa de ar atingem o lado inferior do disco em vários pontos, assimetricamente. Uma aproxima
Admita que o mesmo jato d’água permanente do Problema P 3.40 (velocidade do jato, 8m / s , e diâmetro de 10c m ) atinja uma cavidade em forma de concha, semiesférica, como mostra a Figura P A 3.3 . A
Estenda o problema P3.46 para o problema de calcular o centro de pressão L da força normal F n , como mostra na figura abaixo. (No centro de pressão, não são necessários momentos para manter a placa e