Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 118
Um bocal plano descarrega verticalmente para baixo 1200 L/s por unidade de largura na atmosfera. O bocal é alimentado com um fluxo permanente de água. Uma placa plana estacionária, inclinada, colocada abaixo do bocal é atingida pela corrente de água. A corrente de água divide-se e escoa ao longo da placa inclinada; as duas correntes deiando a placa têm espessuras desiguais. Efeitos de atrito são desprezíveis no bocal e no escoamento ao longo da superfície da placa. Avalie a mínima pressão manométrica requerida na saída do bocal.
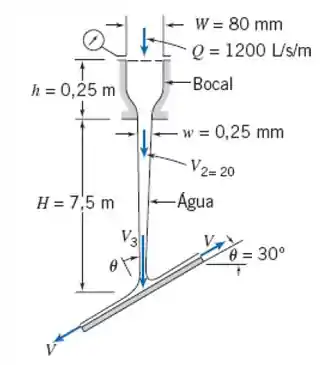
Passo 1
Vamos começar o exercício encontrando a vazão de descarga, que será dada por:
Agora podemos calcular as velocidades 1 e 2 (note que o valor de está errado na figura, na verdade deveria ser )
Agora vamos aplicar Bernoulli entre os pontos 1 e 2:
Tomando a pressão relativa, ou seja, fazendo , isolando e substituindo os valores conhecidos:
Passo 2
Agora vamos aplicar Bernoulli entre os pontos 2 e 3 (placa):
Isolando temos:
Passo 3
Agora vamos aplicar a equação 4.18b apresentada nessa seção do livro para o equilíbrio de momento, então temos:
Como não temos atrito ao longo da placa, então podemos desprezar as forças na direção . Como o escoamento se dá em regime permanente, então a derivada no tempo será zero, dessa forma, substituindo os valores conhecidos, temos:
No entanto, sabemos que a parcela representa a vazão do sistema que é dada por , então, temos: