Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 56
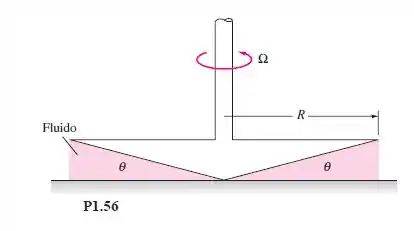
O dispositivo na Figura é chamado de viscosímetro cone-placa. O ângulo do cone é muito pequeno, de forma que , e a folga é preenchida com o líquido de teste. O torque necessário para girar o cone a uma velocidade angular é medido. Considerando um perfil linear de velocidade no filme de fluido, deduza uma expressão para a viscosidade do fluido em função de .
Passo 1
Vamos lá, podemos montar a formula para o torque viscoso.
Para qualquer , o fluído na folga é dada por:
O torque é dado por:
Onde:
Assim:
Agora temos que integrar nosso torque, vamos lá!
Finalizando nossa questão isolando o coeficiente de atrito , temos:
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
Exercícios de Livros Relacionados
O pistão da figura levanta, com velocidade constante, um peso G = 2000N sob a ação de uma pressão. Entre o pistão e o cilindro existe uma película de lubrificante ( ρ = 800k g / m 3 ; v = 10 - 5m 2 /
O dispositivo da figura gira a 1200r p m , acionado por um motor que mantém o torque constante, independentemente da rotação. Para variar a rotação, deloca-se o mancal móvel para a esquerda. Qual a no
Ar escoando verticalmente para baixo atinge uma larga placa plana horizontal. O campo de velocidade é dado por =( a x-a y) ( 2+c o sω t ) , em que a = 5s - 1 , ω = 2 π s - 1 , x e y (medidos em metros
Considere o escoamento descrito pelo campo de velocidade V → = A ( 1+B t ) î +C t y j ^,c o mA = 1m / s î , B = 1 s - 1 eC = 1s - 2 . As coordenadas são medidas em metros. Trace a trajetória da partíc
O campo de escoamento para um escoamento atmosférico é dado por V → = - M y 2 π î + M x 2 π j ^ î em que M=1s - 1 e as coordenadas x e y são paralelas à latitude e longitude locais. Trace um gráfico c