Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 19

Uma pessoa afirma que a vazão volumétrica de um tubo circular com escoamento laminar pode ser determinada medindo a velocidade na linha central da região completamente desenvolvida, multiplicando-a pela área de seção transversal e dividindo o resultado por 2 . Você concorda? Explique.

Passo 1

Para saber se a firmação da pessoa está correta, nós precisamos lembrar da fórmula de vazão volumétrica V ˙ em um tubo. Ela é igual à velocidade média V m é d do escoamento multiplicada pela área da seção transversal do tubo A .

V ˙ = V m é d ⋅ A

Passo 2

No entanto, em um escoamento laminar, a velocidade média V m é d vale metade da velocidade máxima do escoamento V m á x . Substituindo isso na fórmula acima, encontramos:

V ˙ = V m é d ⋅ A       ⟹       V ˙ = V m á x 2 ⋅ A

Passo 3

No entanto, a velocidade máxima V m á x do escoamento laminar completamente desenvolvido é igual à velocidade u r = 0 na linha central do tubo. Isso é visto na figura abaixo.

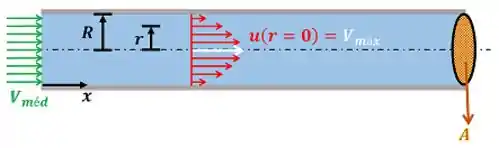
Substituindo isso na fórmula, achamos uma equação par calcular a vazão volumétrica V ˙ em função da velocidade da linha central do tubo u r = 0 .

V ˙ = V m á x 2 ⋅ A     ⟹     V ˙ = u r = 0 2 ⋅ A

Essa equação mostra que de fato se multiplicarmos a velocidade da linha central do tubo u r = 0 pela área da seção transversal do tubo A e dividir o resultado por 2 , achamos a vazão volumétrica V ˙ do escoamento!

Logo, a afirmação da pessoa está correta!

Resposta

Sim, essa conta está correta!

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O perfil da velocidade no escoamento laminar completamente desenvolvido em um tubo circular de raio interno R = 2c m em m / s é dado por u r = 4 ( 1 - r 2 / R ² ) ² . Determine as velocidades média e
Considere o escoamento de óleo com ρ = 894k g / m 3 e μ = 2,33k g / m ∙ s em uma tubulação com 40c m de diâmetro a uma velocidade média de 0,5m / s . Uma seção de 300m de comprimento da tubulação pass
Repita p Problema 8 - 37 para o escoamento turbulento em tubos suaves para os quais o fator de atrito é dado por f = 0,184 R e - 2 . Qual seria a sua resposta para um escoamento totalmente turbulento
Amônia líquida a - 20 ° C escoa através de uma seção de 30m de comprimento de um tubo de cobre com 5m m de deâmetro a uma taxa de 0,15 k g / s . Determine a queda de pressão, a perda de carga e a potê
Em um sistema de aquecimento de ar, o ar aquecido a 40 ° C e 105k P a absoluta é distribuído através de um duto retangular de 0,2m× 0,3m feito de aço comercial a uma taxa de 0,5m ³ / s ³ . Determine a