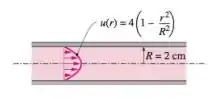
O perfil da velocidade no escoamento laminar completamente desenvolvido em um tubo circular de raio interno R = 2c m em m / s é dado por u r = 4 ( 1 - r 2 / R ² ) ² . Determine as velocidades média e máxima do tubo e a vazão em volume.

u m á x = 4m / s á V m é d i a = 2m / s é V ˙ = 0,00251m 3 / s

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 33

O perfil da velocidade no escoamento laminar completamente desenvolvido em um tubo circular de raio interno em é dado por . Determine as velocidades média e máxima do tubo e a vazão em volume.

Passo 1

Fala aí galera, vamos para mais uma questão de Mecânica dos Fluidos. Primeiramente, vamos determinar as velocidades, para isso, precisamos saber o perfil da velocidade no escoamento laminar desenvolvido em um tubo circular, dado por:

Com isso, podemos comparar esta fórmula com a função que o enunciado nos fornece e, assim, conluir que a velocidade máxima é:

Passo 2

Em seguida, o problema nos pede para encontrarmos a velocidade média. Temos:

Passo 3

Por fim, vamos encontrar a vazão no tubo em volume. Podemos encontrá-la multiplicando a velocidade média pela área da boca circular do tubo, temos:

Substituindo:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O diagrama de Moody dá o fator de atrito de Darcy, f , em termos do número de Reynolds e da rugosidade relativa. O fator de atrito de Fanning para escoamento em tubo é definido como: f F = τ w 1 2 ρ V

Água escoa através de um tubo de 50 mm de diâmetro que subitamente contrai-se para 25 mm. A queda de pressão através da contração é 3,45 kPa. Determine a vazão volumétrica.

Água escoa a 25 L/s através de uma constrição suave, em que o diâmetro do tubo é reduzido de 75 mm para 37,5 mm, segundo um ângulo de 150°. Se a pressão antes da constrição for 500 kPa, estime a press

Ar escoa para fora de uma câmara de teste de uma sala limpa através de um duto de 150 mm de diâmetro e de comprimento L. O duto original tinha uma entrada de borda-viva, mas essa foi substituída por o

Um difusor cônico, com 150 mm de comprimento, é usado para expandir um tubo de um diâmetro de 50 mm para um diâmetro de 89 mm. Para uma vazão de água de 47 L/s, estime o aumento na pressão estática. Q