Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 31
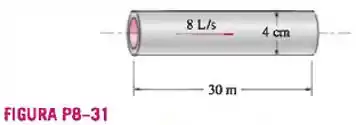
Água a ( e ) escoa em regime permanente em um tubo horizontal com de diâmetro e de comprimento feito de aço inoxidável a uma taxa de . Determine (a) a queda de pressão, (b) a perda de carga e (c) o requisito de potência de bombeamento para superar essa queda de pressão.
Passo 1
Antes de começar a questão, devemos notar que o diâmetro e o comprimento do tubo informado pelo enunciado da questão está diferente do diâmetro e do comprimento do tubo informado pela figura P8-31. Para conseguirmos fazer o exercício, escolhemos usar os dados da ffigura ao invés dos dados do texto.
A questão pede primeiro para a gente calcular a queda de pressão através do tubo. O primeiro passo para calcular o da água através do tubo é calcular o número de Reynolds do escoamento. Se o escoamento for laminar, usaremos uma fórmula para , se ele for turbulento, usaremos outra. A equação do número de Reynolds segue abaixo.
onde é a densidade do fluido (que vale ), é a viscosidade do fluido (que vale ), (que vale ou ) é o diâmetro do tubo e é a velocidade média do escoamento. Podemos calcular a velocidade média dividindo a vazão volumétrica dada pelo enunciado ( ou ) pela área da seção transversal do tubo ( vale , porque o tubo é circular).
Substituindo os dados na fórmula de , achamos:
Quando o é menor que , o escoamento é laminar. Quando é maior que , ele é turbulento. Vemos que no nosso caso, é maior que . Logo, o escoamento da água é turbulento.
Passo 2
A fórmula da queda de pressão se encontra abaixo (equação 8-21 do livro).
onde é o fator de atrito e é o comprimento do tubo (que vale ).
Para calcular esse fator de atrito em um escoamento turbulento, reorgazinamos a equação 8-51 do livro feita para calcular fator de atrito de escoamentos turbulentos.
onde é o tamanho da rugosidade do tubo. O valor de é encontrado na tabela 8-2 do livro para tubos de vários materiais. Como no nosso caso o tubo é feito de aço inoxidável, vale:
Substituindo os dados na fórmula de fator de atrito , encontramos:
Colocando esse valor na fórmula de , achamos:
Passo 3
Sabendo quanto vale , a questão pede agora para a gente calcular a perda de carga do escoamento do tubo. A fórmula para calcular em função de é mostrada abaixo (equação 8-24).
Substituindo os valores que temos nessa equação, encontramos:
Passo 4
Por fim, o problema pede para a gente calcular o requisito de potência de bombeamento para superar essa queda de pressão que calculamos . A equação de potência de bombeamento segue abaixo.
onde é a vazão volumética de água através do tubo.
Usando os dados que temos: