92 - Uma placa de circuito com de espessura, de altura e de comprimento abriga chips lógicos espaçados de um lado, cada um dissipando . A placa é impregnada com recheios de cobre e possui uma condutividade térmica eficaz de .Todo o calor gerado nos chips é conduzido através da placa de circuito e é dissipado da parte traseira da placa para o ar ambiente a , que é forçado a fluir sobre a superfície por um ventilador a uma velocidade de fluxo livre de . Determine as temperaturas nos dois lados da placa de circuito.
Passo 1
Desenhe o esquema da placa de circuito, conforme mostrado na figura a seguir:
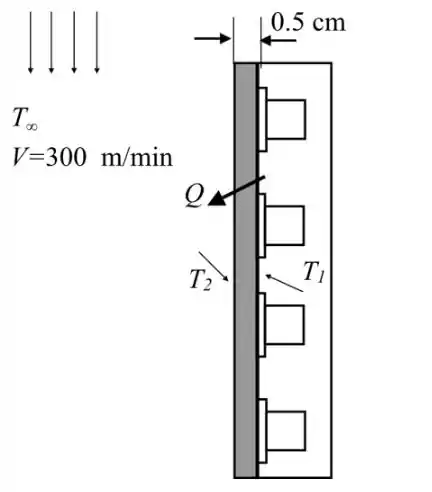
Passo 2
A temperatura na parte externa da placa deve ser maior que a temperatura ambiente .Por isso, vamos assumir uma temperatura de filme como sendo . Portanto para e temos:
Condutividade térmica é:
Viscosidade cinemática é:
O número Prandtl é:
Passo 3
O número de Reynolds para o fluxo é determinado a partir da equação dada por:
Como , o fluxo é considerado laminar.
O número de Nusselt é calculado usando a relação à baixo:
Passo 4
O coeficiente convectivo de transferência de calor do ar é determinado a partir da equação dada por:
Reescreva para achar :
Passo 5
Da equação do balanço de energia, temos:
Aqui é a área de transferência de calor, é a altura, é o número de chips, é o calor total dissipado, é o calor dissipado por cada chip e é o comprimento da placa.
Substituindo pelos valores conhecidos, temos:
Portanto, a temperatura no lado externo do painel é .
Passo 6
Calcule a temperatura no interior da placa, considerando a expressão para taxa de transferência de calor.
Aqui, é a espessura da placa.
Portanto, a temperatura no lado interno do painel é .
Resposta
A temperatura no lado externo do painel é .
A temperatura no lado interno do painel é .