Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 9.Exercício - Ex. 13

Uma placa de 0,9 m x 1,2 m move-se com 13,2 m/s em ar parado, com uma inclinação de 12º com a horizontal. Sendo C a = 0,17 ; C s = 0,72 ; ρ = 1,2   k g / m 3 ; A=área de referência = área da placa, determinar:

  1. A força resultante exercida pelo ar sobre a placa;
  2. A força de atrito
  3. A potência necessária para manter a placa em movimento.

Passo 1

Dados da questão:

  • Dimensões da placa: 0,9   m   x   1,2   m
  • Velocidade da placa: v = 13,2   m / s
  • Coeficiente de arrasto: C a = 0,17
  • Coeficiente de sustentação: C s = 0,72
  • Densidade do ar: ρ = 1,2   k g / m 3

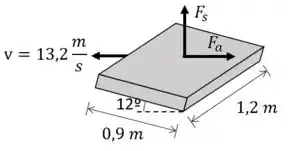
Passo 2

A área de referência é igual a área de superfície da placa:

A = 1,2 ⋅ 0,9 = 1,08   m 2

Passo 3

A força resultante exercida pelo ar sobre a placa é a soma vetorial da força de arrasto e da força de sustentação:

Força de arrasto:

F a = C a ⋅ ρ ⋅ v 0 2 2 A = 0,17 ⋅ 1,2 ⋅ 13,2 2 2 ⋅ 1,08

F a = 19,19   N

Força de sustentação:

F s = C s ⋅ ρ ⋅ v 0 2 2 A = 0,72 ⋅ 1,2 ⋅ 13,2 2 2 ⋅ 1,08

F s = 81,29   N

Logo a força resultante é:

F r = F s 2 + F a 2 = 81,29 2 + 19,19 2

F r = 83,52   N

Passo 4

Vamos decompor as forças de arrasto e de sustentação na direção da placa para encontrar a força de atrito F a t

F a t = F a ⋅ cos ⁡ 12 º - F s ⋅ cos ⁡ 78 º

F a t = 19,19 ⋅ cos ⁡ 12 º - 81,29 ⋅ cos ⁡ 78 º

F a t = 1,87   N

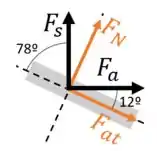
Passo 5

Para manter a placa em movimento é preciso gerar potência suficiente para vencer a força de arrasto:

N = F a ⋅ v

N = 19,19 ⋅ 13,2

N = 253,31   W

N = 0,25   k W

Resposta

F r = 83,52   N

F a t = 1,87   N

N = 0,25   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma rede de pesca é feita com fio de nylon com 0,75m m de diâmetro, e tecida em formato retangular. As distâncias, vertical e horizontal, entre as linhas de centro dos fios adjacentes são de 1 c m . E
Uma folha de material plástico, com espessura de 10 m m e S G = 1,5 , é deixada cair dentro de um grande tanque contendo água. A folha tem 0,5mx1m . Estime a velocidade terminal da folha, quando ela c
A resistência de uma barcaça deve ser determinada a partir de testes com modelos. O modelo é construído em uma razão de escala de 1 : 13,5 e tem comprimento, través e calado de 7,00m ,1,4m e 0,2m , re
O seguinte ajuste de curva para o coeficiente de arrasto de uma esfera lisa em função do número de Reynolds foi proposto por Chow [36]:Use os dados da Fig. 9.11 para estimar a magnitude e a localizaçã
Um balão esférico de 0,6m de diâmetro, cheio de hidrogênio, exerce uma força vertical de 1,3N sobre a corda que o retém, quando mantido estacionário no arpadrão sem vento. Com uma velocidade do vento