Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 9.Exercício - Ex. 3

Um balão contém hélio e é lançado no ar, que no local tem massa específica. O balão mais os acessórios pesam 240 π   N . Escolher, entre os diâmetros indicados a seguir, aquele que permite uma ascensão com a velocidade mais próxima de 10 m/s. Escolhido o diâmetro, verificar qual será a velocidade real de subida, supondo o coeficiente de arrasto 0,266 . Se o balão é ancorado ao solo e é atingido por um vento de 35   k m / h , determine o ângulo que o cabo de ancoragem formará com o solo. Diâmetros (m): 4,8; 5,2; 5,6; 6,0; 6,4

Passo 1

A questão nos dá:

  • Densidade do ar ρ = 1,2   k g / m 3 .
  • Peso total do balão: P = 240 π   N .
  • Velocidade relativa: v 0 = 10   m / s .
  • Coeficiente de arrasto: C a = 0,266
  • Velocidade do vento: v v e n t o = 35 k m h ≈ 10 m s .

A questão pede:

  • O diâmetro do balão: D = ?
  • Ângulo entre o solo e o cabo de ancoragem: α = ?

Passo 2

Vamos começar pelo processo de subida do balão! Nesta situação, a corda não está esticada, então ela não oferece nenhuma tração ou resistência.

Enquanto o balão sobe, duas forças o puxam pra baixo: A força peso P e a força de arrasto F a . A força que faz o balão subir é a flutuabilidade E , como o hélio é mais leve que o ar, então o balão tende a flutuar no ar. O diagrama de corpo livre com as três forças é indicado:

E = F a + P

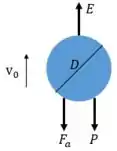
  • A flutuabilidade é dada por E = ρ f l u i d o ⋅ g ⋅ V d e s l o c a d o
  • A força de arrasto é dada por: F a = C a ⋅ ρ a r ⋅ v 0 2 2 A
  • O volume deslocado por uma esfera é: V d e l o c a d o = 1 6 π D 3
  • E a área de referência de uma esfera é: A = π D 2 4

Substituindo as equações:

ρ a r ⋅ g ⋅ 1 6 π D 3 = C a ⋅ ρ a r ⋅ v 0 2 2 ⋅ π D 2 4 + P

Aplicando os valores:

1,2 k g m 3 ⋅ 10 m s 2 ⋅ 1 6 π D 3 = 0,266 ⋅ 1,2 k g m 3 ⋅ 10 m s 2 2 ⋅ π D 2 4 + 240 π

D 3 = 1,995 D 2 + 120

Chegamos em uma equação do terceiro grau:

D 3 - 1,995 D 2 - 120 = 0

Passo 3

D 3 - 1,995 D 2 - 120 = 0

Não precisamos resolver a equação acima. Podemos substituir os diâmetros que a questão ofereceu e ver qual valor mais se aproxima de zero:

O diâmetro que mais aproxima a equação de zero é:

D = 5,6   m

Passo 4

Agora, podemos calcular a verdadeira velocidade de subida do balão:

E = F a + P

ρ a r ⋅ g ⋅ 1 6 π D 3 = C a ⋅ ρ a r ⋅ v 0 2 2 ⋅ π D 2 4 + P

1,2 k g m 3 ⋅ 10 m s 2 ⋅ 1 6 π ⋅ 5,6 3 = 0,266 ⋅ 1,2 k g m 3 ⋅ v 0 2 2 ⋅ π ⋅ 5,6 2 4 + 240 π

351,232 π = 1,251264 π ⋅ v 0 2 + 240 π

v 0 = 9,43 m s

Passo 5

Agora vamos considerar a situação em que o balão atingiu uma altura estável! Nesta situação o vento é de 35   k m / h . Vamos assumir que está velocidade é de aproximadamente v v e n t o = 10   m / s

Nessa situação a corda está esticada e uma força de tração T atua sobre ela. Um vento lateral atuando sobre o balão gera uma força de arrasto F a . Como o balão é menos denso que o ar, existe uma força de flutuação E e o peso P do balão.

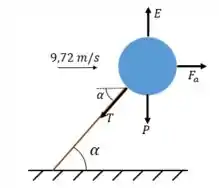
Como esta é uma situação estática, temos:

∑ F x = 0 ⇒ F a - T ⋅ cos ⁡ α = 0

∑ F y = 0 ⇒ E - P - T ⋅ sen ⁡ α = 0

Isolando o α

cos ⁡ α = F a T

sen ⁡ α = E - P T

Dividindo o seno pelo cosseno:

sen ⁡ α cos ⁡ α = E - P T F a T

Chegamos em:

tan ⁡ α = E - P F a

Passo 6

tan ⁡ α = E - P F a

Aplicando as equações:

tan ⁡ α = ρ a r ⋅ g ⋅ 1 6 π D 3 - P C a ⋅ ρ a r ⋅ v 0 2 2 ⋅ π D 2 4

tan ⁡ α = 1,2 k g m 3 ⋅ 10 m s 2 ⋅ 1 6 π ⋅ 5,6 3 - 240 π 0,266 ⋅ 1,2 k g m 3 ⋅ 10 m s 2 2 ⋅ π ⋅ 5,6 2 4

tan ⁡ α = 0,889

α = 41,63 º

Resposta

D = 5,6   m

α = 41,63 º

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um avião pesa 18 kN e tem uma área de asa de 27m 2 . Qual deverá ser o ângulo de ataque das asas a uma velocidade de 160 km/h? Supor que o coeficiente de sustentação varie linearmente de 0 º º a 6º de
Um anemômetro, utilizado para medir a velocidade do vento, consiste de duas semiesferas ocas montadas em sentidos opostos sobre dois braços iguais, que podem girar livremente quando montados sobre um
Um papagaio pesa 1 N e tem uma área de 74,4d m 2 . A tensão na linha é 30 N quando ela forma um ângulo de 45º com a direção do vento. Para um vento de 36 km/h, quais serão os coeficientes de arrasto e
Uma bola de beisebol é disparada para cima com uma velocidade inicial de 25m / s . A bola de beisebol tem um diâmetro de 0,073m e uma massa de 0,143k g . O coeficiente de arrasto para a bola de beiseb
Alguns carros são equipados de fábrica com um spoiler, uma seção de asa instalada na traseira do veículo que as revendedoras afirmam aumentar significativamente a tração dos pneus em alta velocidade.