Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 116

Uma placa plana coberta por uma substância volátil (espécie A) está exposta a um escoamento paralelo de ar atmosférico seco a T∞ = 20°C e com u∞ = 8 m/s. A placa é mantida a uma temperatura constante de 134°C por um elemento aquecedor elétrico e a substância evapora da superfície. A placa possui uma largura de 0,25 m (normal ao plano da figura) e sua superfície inferior encontra-se isolada.

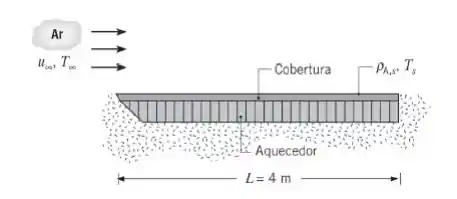
A massa molar e o calor latente de vaporização da espécie A são MA = 150 kg/kmol e hlv = 5,44 × 10 6 J/kg, respectivamente, e a difusividade mássica é de DAB = 7,75 × 10 −7 m2 /s. Se a pressão do vapor saturado da espécie é de 0,12 atm a 134°C, qual é a potência elétrica necessária para manter o sistema em condições de regime estacionário?

Passo 1

Fala aí! Partiu resolver essa questão! Nosso enunciado quer saber o tempo que a potência elétrica necessária para o sistema se manter em regime estacionário, show?

Podemos encontrar o que ele pede da seguinte forma:

q = q c o n v e c ç ã o + q e v a p o r a ç ã o

q = h _ L   .   A s   .   T   s - T   ∞ + h _ m ,   L   .   A s   .   ρ A ,   s - ρ A ,   ∞ .   h f g

Precisamos fazer algumas continhas antes, para encontrar os termos que nos faltam… Mas antes disso, vamos visitar a tabela A-4, do apêndice do livro, para pegar mais algumas informações, usando a temperatura média e a pressão dada:

k a r = 0,030   W / m . K v = 20,92   .   10 - 6   m ² / s P r = 0,700

M A = 150   k g / k m o l p A ,   s a t = 0,12   a t m D A B = 7,75   .   10 - 7   m ² / s

h f g = 5,44   .   10 6   J / k g

Vamos lá então!

Passo 2

Agora vamos fazer nossa sequência de continhas para encontrar o h L _ e o h m ,   L _ , partiu!

Então vamos começar encontrando o número de Reynolds:

R e = u ∞   .   L v

R e = 8   .   4 20,92   .   10 - 6

R e = 1,530   .   10 6

Agora o valor de N u _ L :

N u _ L = 0,037 . R e L 4 / 5 - 871 . P r 1 / 3

N u _ L = 0,037 . 1,530   .   10 6 4 / 5 - 871 . 0,700 1 / 3

N u _ L = 2140

Vamos continuar…

Passo 3

Agora sim podemos encontrar o h L _ e o h _ m ,   L :

h _ L = N u _ L   .   k L

h _ L = 2140   .   0,030 4

h _ L = 16   W / m ² . K

Vamos continuar:

h _ m ,   L = h _ L . D A B k . S c P r 1 / 3

h _ m ,   L = 16 . 7,75   .   10 - 7 0,030 .   20,92   .   10 - 6 7,75   .   10 - 7 0,700 1 / 3

h _ m ,   L = 0,00140   m / s

Estamos quase lá, mas ainda falta o valor de ρ A ,   s :

ρ A ,   s = p A ,   s R M A . T s

ρ A ,   s = 0,12 8,205   .   10 - 2 150 . 134 + 273

ρ A ,   s = 0,539   k g / m ³

Passo 4

Show! Vamos finalizar nossa questão:

q = 16   .   4.0,25 .   134 - 20 + 0,00140   .   4.0,25   .   0,539 - 0 .   5,44   .   10 6

q = 5,93   k W

Uhul! Conseguimos!

Resposta

q = 5,93   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

73. Um termossifão é formado por um recipiente fechado que absorve calor ao longo de sua seção de ebulição e rejeita calor ao longo de sua seção de condensação. Considere um termossifão formado por um
72. Uma técnica passiva para o resfriamento de circuitos integrados (CIs) que dissipam calor envolve a submersão dos CIs em um fluido dielétrico com baixo ponto de ebulição. O vapor gerado no resfriam
69. Refrigerante R-22, a uma vazão mássica de = 8,75 × 10–3 kg/s, é condensado no interior de um tubo com 7 mm de diâmetro. Observa-se escoamento anular. A temperatura de saturação do refrigerante pre
77. Foi proposto que o ar muito quente retido no interior do sótão de uma casa no verão pode ser usado como a fonte de energia para um aquecedor de água passivo instalado no sótão. Custos com energia
Quando uma lâmina de aço deixa a última série de rolos em um processo de laminação a quente, antes de ser bobinada, ela é temperada com a utilização de jatos planos de água. Devido às elevadas tempera