Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 32
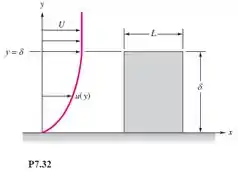
Uma placa plana de comprimento L e altura é colocada em uma parede paralelamente a uma camada-limite que se aproxima, como na Figura P7.32. Admita que o escoamento sobre a placa seja totalmente turbulento e que o escoamento de aproximação siga a lei da potência um sétimo
Aplicando uma teoria para tiras de largura dy e comprimento L, deduza uma fórmula para o coeficiente de arrasto dessa placa. Compare esse resultado com o arrasto na mesma placa imersa em um escoamento uniforme
Passo 1
E vamo lá pra mais uma!
Cara, temos uma tirinha de largura dy, certo?! Ela tem um comprimento L, essa tira ta sujeita a uma corrente , logo a força de arraste nela será de:
Onde, é dado por:
Vamos colocar isso dentro de e integrar, assim:
Assim,
Essa força é (49/62), ou 79%, da força na mesma placa se ela tivesse imersa em uma corrente uniforme!