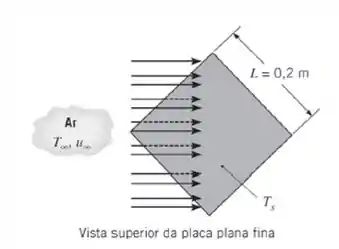
Uma placa plana fina, com de lado, e superfícies superior e inferior rugosas, encontra-se posicionada em um túnel de vento de tal forma que suas superfícies estão paralelas a uma corrente de ar atmosférico com uma velocidade de . O ar está a uma temperatura de , enquanto a placa é mantida a . A placa está rodada em em torno de seu ponto central, como mostrado no esquema. Ar escoa sobre as superfícies superior e inferior da placa e medidas da taxa de transferência de calor indicam . Qual é a força de arrasto na placa?

A força de arrasto na placa se dá por:

Com:

Então:

Substituindo do Passo 1, obtemos:

Temos por definição:

Substituindo na equação do Passo 2:

A difusividade térmica é expressa por:

Substituindo na equação de força de arrasto:

O número de Prandtl é dado como:

Substituindo na equação do Passo 3:

Por fim, a taxa de transferência de calor por convecção é:

Realizando a última substituição:

Calculando a temperatura de filme:

Dados:

;

.

Temos

Na Tabela obtemos as seguintes propriedades do ar sob a temperatura de filme de 50°C (323 K):

Dados:

;

;

.

Temos: