Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 5.Problemas - Ex. 119
Uma placa unidimensional com espessura 2L está inicialmente a uma temperatura uniforme 7). De repente, uma corrente elétrica é passada através da placa, causando um aquecimento volumétrico uniforme j(W/m3 ). No mesmo instante, as duas superfícies externas ( x = ± L)são submetidas a um processo de convecção a T„, com um coeficiente de transferência de calor h.
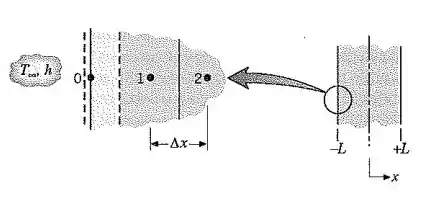
Escreva a equação de diferenças finitas que representa a conservação de energia no nó0, localizado na superfície externa em x — —L. Reordene a sua equação e identifique alguns coeficientes adimensionais importantes.
Passo 1
Fala aí galerinha? Tudo bem com vocês? Bora pra cima! O que sabemos das condições iniciais?
Parede unidimensional repentinamente submetida a aquecimento volumétrico uniforme e condições de superfície convectiva. Vamos resolver a partir do método implícito.
Método Implícito. Começaremos fazendo um balanço de energia. Na Eq. abaixo, entretanto, as temperaturas no LHS são avaliadas no novo tempo (p+1). O RHS fornece uma aproximação de diferença regressiva para a derivada de tempo.
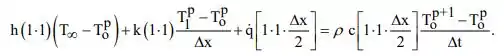
Logo,
Ou,