Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 5.Problemas - Ex. 38
Considere o duto bem isolado termicamente do Exemplo 5.4, que é subitamente sujeito ao escoamento de um óleo quente. Use uma rotina computacional para a condução transiente em paredes planas para obter os resultados a seguir.
(a) Calcule as temperaturas das superfícies interna e externa do duto, o fluxo térmico na superfície interna e a energia transferida para a parede após 8 min. Compare os seus resultados com aqueles obtidos no exemplo.
(b) Em que tempo a temperatura da superfície externa do duto, 7X0, f), atingirá 25°C?
(c) Com a sua rotina, calcule e represente graficamente em um único gráfico as distribuições de temperaturas, \ T x,t),na condição inicial, na condição final e nos tempos intermediários de 4 e 8 min. Explique características importantes das distribuições.
(d) Calcule e represente graficamente o histórico das temperaturas, T( x, t), nas superfícies interna (x = 0) e externa (x = L) do duto para 0 t 16 min.
Passo 1
Fala aí galerinha? Tudo bem com vocês? Bora pra cima! Temos que a parede do tubo está sujeita a uma mudança repentina na condição da superfície convectiva. Veja o exemplo 5.4. O modelo IHT representa a solução em série para a parede plana fornecendo temperaturas e fluxos de calor avaliados em (x,t) e a energia total transferida no interior da parede em (t).
No item b) Para determinar o tempo para o qual T(0,t) = 25°C, o modelo IHT é resolvido para após definir x = 0 e T_xt = 25°C. Encontramos então, para = 4,4 min.
Passo 2
Avaliando os coeficientes e resolvendo as equações simultaneamente, a distribuição de temperatura em estado estacionário (°C), tabulada de acordo com as localizações dos nós, é:
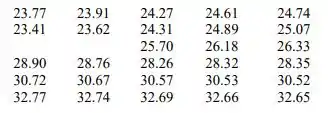
Alternativamente, os resultados anteriores podem ser facilmente obtidos acessando o painel IHT Tools e usando as opções 2-D, SS, equações diferenciais finitas, as equações do modelo estão anexadas). As temperaturas máxima e mínima da placa fria estão nos locais inferior (T24) e superior central (T1), respectivamente.
(b) Para as condições prescritas, a temperatura máxima permitida (T24 = 40°C) é atingida quando o
As opções para estender esse limite podem incluir o uso de uma placa fria de cobre (k ≈ 400 W/m⋅K) e/ou aumentar o coeficiente de convecção associado ao refrigerante. Com
, um valor de pode ser mantido.
Com
(um limite superior prático), q′′o = 28,65 W/cm2.
Melhorias adicionais, embora pequenas, podem ser realizadas realocando os canais de refrigeração mais perto da base da placa fria.
Resposta
Resposta nos passos