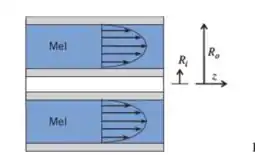
Em uma planta de processamento de alimentos, mel é bombeado em um espaço anular de comprimento L = 2 m e com raio interno Ri = 5 mm e raio externo Re = 25 mm. A diferença de pressão aplicada é Δp = 125 kPa e a viscosidade do mel é μ = 5 N · s/m2. O perfil teórico de velocidade para o escoamento laminar através de um espaço anular é:

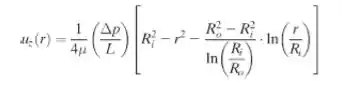
Mostre que a condição de não deslizamento é satisfeita por essa expressão. Determine a localização em que a tensão de cisalhamento é zero. Determine a força viscosa atuando nas superfícies interna e externa, e compare esses valores com a força Δpπ(Ro2 − Ri2). Explique.

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. O nosso problema quer que a gente mostre que a condição de não deslizamento é satisfeita pela expressão que foi dada e quer que a gente determine a localização em que a tensão de cisalhamento é zero e a força viscosa atuando nas superfícies interna e externa… Ou seja, é bastante coisa, mas a gente consegue dar conta!

Sabemos que o perfil de velocidade é dado por:

Aplicando as condições de contorno, temos que em , a velocidade será:

Aplicando a propriedade de logaritmo que o log da divisão é a subtração de logs, teremos:

Agora a ideia é tentar cortar o termo com ln’s do numerador com o do denominador, para isso, vamos fazer a seguinte alteração no termo do numerador:

Fazendo isso, vamos conseguir cortar esse termo com o do denominador, saca só:

E agora, é só cortar...

Logo:

E a segunda condição de contorno, em , vai nos dar:

Aqui, temos que , portanto:

Então:

Logo, a condição de não deslizamento é satisfeita pela equação.