Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 55

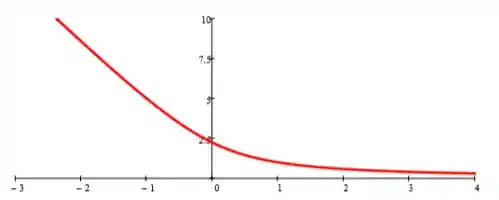
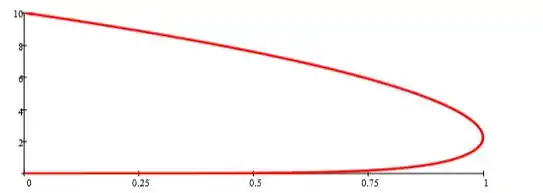
Óleo SAE 10W30 a 100°C é bombeado através de um tubo de comprimento L = 10 m e diâmetro D = 20 mm. A diferença de pressão aplicada é Δp = 5 kPa. A linha de centro do tubo é um filamento metálico de diâmetro d = 1 μm. O perfil teórico de velocidade para o escoamento laminar através do tubo é:

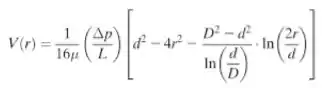
Mostre que a condição de não deslizamento é satisfeita por essa expressão. Determine a localização em que a tensão de cisalhamento é zero. Trace os gráficos das distribuições da velocidade e da tensão. (Para a curva da tensão, defina um limite superior de tensão de 5 Pa.) Discuta os resultados.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Sabemos que o perfil de velocidade é dado por:

V r = 1 16 μ ∆ p L d ² - 4 r 2 - D ² - d ² ln ⁡ d D ln ⁡ 2 r d  

Aplicando as condições de contorno:

r = D 2

V D 2 = 1 16 μ ∆ p L d ² - D ² + D ² - d ² = 0

r = d 2

u z R i = 1 16 μ ∆ p L 0 = 0

Logo, a condição de não deslizamento é satisfeita pela equação.

Passo 2

A localização na qual a tensão é nula é dada por:

τ = μ d u d r

Derivando a expressão do passo 1 e igualando a 0, teremos:

r = 2,25 m m

Traçando a curva de posição por tensão:

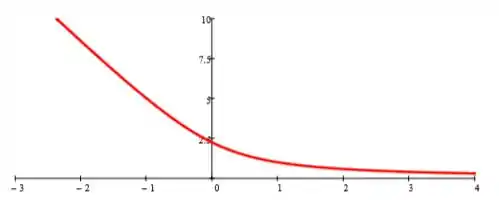
Já a curva de posição por velocidade:

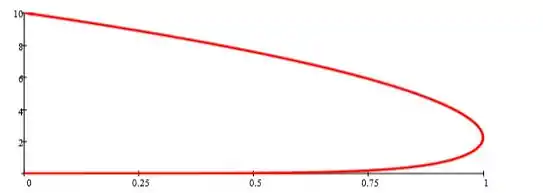
Logo:

τ D 2 = - 2,374 P a

τ d 2 = 2,524 k P a

Resposta

r = 2,25 m m

τ D 2 = - 2,374 P a

τ d 2 = 2,524 k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco com dimensões de 50c m × 30c m × 20c m pesando 150N deve ser deslocado com a velocidade constante de 0,8m / s num plano inclinado com o coeficiente de atrito 0,27 . ( a ) Determine a força F
Reconsidere o Problema 2-44. Investigue o efeito da espessura da película de óleo sobre o torque transmitido, usando o programa EES (ou outro similar). Suponha que a espessura da película de óleo vari
Considere o escoamento de um fluido com viscosidade μ através de um tubo circular. O perfil de velocidade no tubo é expresso por u r = u m á x ( 1 - r n / R n ) á , onde u m á x á é a velocidade máxim
A viscosidade de alguns fluidos muda quando um campo elétrico é aplicado sobre eles. Tal fenômeno é conhecido como efeito reológico (ER) e os fluidos que apresentam tal comportamento são denominados f
Um corpo com forma de tronco de cone está girando com velocidade angular constante de 200 rad/s num recipiente cheio de óleo S A E10 W a 20 ° C μ = 0,1P a ∙ s , como mostrado na Figura P2-43. Se a esp