Enunciado
Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 62
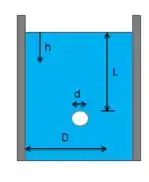
O pórtico circular de acesso na lateral de um reservatório vertical de água tem diâmetro de 0,6 m e está fixado por oito parafusos igualmente espaçados em torno da circunferência. se o diâmetro da coluna de água no reservatório é 7 m e o centro do pórtico está localizado a 12 metros abaixo da superfície livre da água, determine (a) a força total sobre o pórtico e (b) o diâmetro adequado do parafuso.
Passo 1
Temos nessa questão que a porta é mantida no lugar por oito parafusos espaçados uniformemente em torno da circunferência do porto. O centro do porto está localizado a uma distância conhecida abaixo da superfície livre de a água.
O nosso objetivo é encontrar o que é pedido e para isso aplicaremos as equações hidrostáticas neste sistema, sendo:
, referente a pressão hidrostática ( é positivo para baixo)
, força hidrostática
, tensão normal no parafuso
E, por fim, fazemos algumas considerações: um problema de estática dos fluidos; fluido incompressível; a força é distribuída uniformemente por todos os parafusos; a tensão de trabalho adequada nos parafusos é de 100 MPa; a pressão atmosférica atua na superfície livre da água e fora do porto.
Passo 2
Para os cálculos, começa-se integrando a equação da pressão hidrostática. Assim, a força resultante na porta é:
Substituindo os dados, temos:
Passo 3
Na letra (b), para encontrar o diâmetro do parafuso, consideramos a tensão normal, onde A é a área de todos os parafusos:
Logo, .
Igualando a área à tensão, temos
Resposta
(a)
(b)