Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 82

Uma superfície curva é formada com um quadrante de um cilindro circular de raio R   =   0,750   m , conforme mostrado. A superfície tem largura w   =   3,55   m . Água permanece à direita da superfície até uma profundidade H   =   0,650   m . Calcule a força hidrostática

vertical sobre a superfície curva. Avalie a linha de ação dessa força. Determine o módulo e a linha de ação da força horizontal sobre a superfície.

Passo 1

Nessa questão temos uma superfície curva, com raio R e largura w , em que há uma substância (água) na profundidade H . Devemos encontrar a magnitude e linha de ação das forças vertical e horizontal nas curvas.

Agora vamos ver com quais expressões podemos calcular isso:

d p d h = ρ g , pressão hidrostática onde h é positivo para baixo.

F v = ∫ p d A y , força hidrostática vertical

F H = p c A , força hidrostática horizontal

x ' F V = ∫ x d F V

h ' = h c + I x x h c A , linha de ação da força horizontal.

Como todo problema da MecFLu, fazemos algumas considerações: fluido estático e incompressível; pressão atmosférica atuando na superfície livre da água e no lado esquerdo da superfície curva.

Passo 2

Vamos começar integrando a equação da pressão hidrostática.

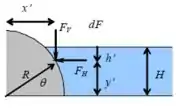
A partir da geometria, temos: y = R sin ⁡ θ , x = R cos ⁡ θ , h = H - R sin ⁡ θ e d A = w R   d θ ; onde θ 1 = asin ⁡ d R = 1,048 .

Assim, podemos aplicar na equação para a força vertical:

F v = ∫ p d A y

F v = ∫ 0 θ 1 ρ g   ( H - R sin ⁡ θ ) sin ⁡ θ w R   d θ

F v = ρ g w R ∫ θ 1 π 2 [ H sin ⁡ θ - R sin ⁡ θ 2 ]   d θ

F v = ρ g w R H 1 - cos ⁡ θ 1 - R θ 1 2 - sin ⁡ 2 θ 1 4

Substituindo os valores temos:

F v = 999 × 9,81 × 3,55 × 0,75 0,65 1 - cos ⁡ ( 1,048 ) - 0,75 1,048 2 - sin ⁡ 2 × 1,048 4

F v = 2,47   k N

Para calcular a linha de ação, fazemos aplicando na fórmula para a força vertical:

x ' F V = ρ g R 2 w H 2 × sin ⁡ θ 1 2 - R 3 × sin ⁡ θ 1 3

Assim, podemos encontrar por:

x ' = x ' F V F v = ρ g R 2 w F v H 2 × sin ⁡ θ 1 2 - R 3 × sin ⁡ θ 1 3

Agora é só resolver normalmente:

x ' = 1 2,47 k N × 999 × 9,81 m s 2 × ( 0,750 ) 2 × 3,55 0,650 2 × 0,650 0,750 2 - 0,750 3 × 0,650 0,750 3

x ' = 0,645   m

Passo 3

Para a força horizontal, nos usamos a formula F H = p c A , substituindo o que dse pede:

F H = ρ g h c H w

Dividimos a altura:

F H = ρ g H 2 H w

Agora é só substituir os dados:

F H = 999 k g m 3 × 9,81 m s 2 × 0,650   m 2 × 0,650   m × 3,55   m = 7,35   k N

E, por ultimo, para a linha de ação, usamos a expressão dada no passo 1, onde I x x = w H 3 12 e a área A = w H , logo

h ' = h c + I x x h c A

h ' = H 2 + w H 3 12 × 2 H × 1 w H

h ' = 0,650   m 2 + 3,55   m ( 0,650   m ) 3 12 × 2 0,650   m × 1 3,55   m × 0,650   m

h ' = 0,433   m

Prontinho!!

Resposta

F v = 2,47   k N

x ' = 0,645   m

F H = 7,35   k N

h ' = 0,433   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma comporta retangular (de largura w = 2 m) é articulada conforme mostrado, com um batente na borda inferior. Em que profundidade H a comporta estará prestes a abrir?
Uma comporta plana semicircular AB, articulada ao longo de B, é suportada pela força horizontal FA aplicada em A. O líquido à esquerda da comporta é água. Calcule a força FA requerida para o equilíbri
Uma comporta plana, de espessura uniforme, suporta uma coluna de água conforme mostrado. Determine o peso mínimo da comporta necessário para mantêla fechada.
Uma seção de parede vertical deve ser construída com mistura pronta de concreto derramada entre formas. A seção de parede tem 3 m de altura, 0,25 m de espessura e 5 m de largura. Calcule a força exerc
Uma sólida represa de concreto deve ser construída de modo a reter água até uma profundidade D . Para facilitar a construção, as paredes da represa devem ser planas. Sua supervisora solicita que você