Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 8
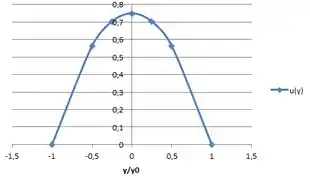
Em uma posição axial específica, os perfis de velocidades e de temperaturas para o escoamento laminar em um canal entre placas paralelas têm as formas:
Com unidades de m/s e °C, respectivamente.
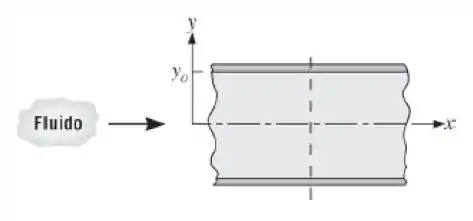
Determine os valores correspondentes para a velocidade média, , e para a temperatura média (ou média de mistura), . Represente graficamente as distribuições de velocidades e de temperaturas. Os valores obtidos por você para e parecem razoáveis?
Passo 1
Faaaaaaaaaaaaalaa galerinha!!
Bora continuar?!
Vamos começar relembrando, como se calcula a velocidade média?
No nosso querido Incropera nos diz que para o fluxo laminar entre placas paralelas:
Sabemos que a área da seção transversal é dada em função do comprimento, L, e da largura entre as placas paralelas, W:
De acordo com a figura:
Se derivarmos em relação a y:
Substituindo:
O problema já nos disse que:
Então:
Rearranjando para facilitar a nossa vidaa :
Passo 2
Agora que temos a velocidade média vamos achar a temperatura média, vamos ver a fórmula?
Substituindo o que já achamos aqui:
Reorganizando aqui também:
Passo 3
Mas não acabamos, certo? Precisamos traçar o perfil da velocidade e temperatura e para isso vamos usar o que o problema nos disse:
Quando fazemos uma tabelinha com as nossas respostas:
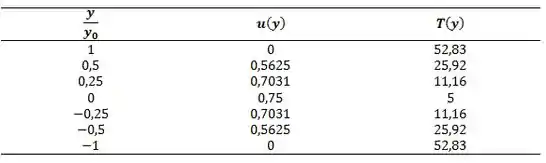
Lançando no gráfico:
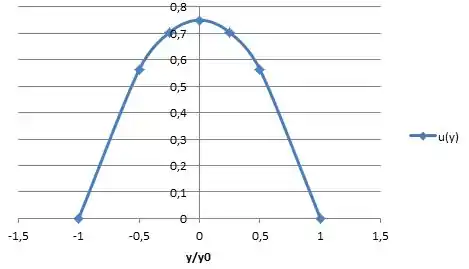
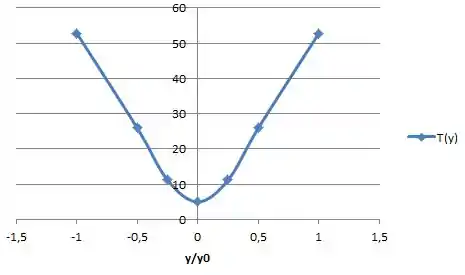
E assim nós acabamos mais umaa !!
Resposta
