Nos Problemas 12.20 e 12.25, estimamos a temperatura da superfície da Terra supondo que a Terra fosse negra. A maioria da superfície da Terra é água, que tem uma emissividade hemisférica de ε = 0,96. Na realidade, a superfície da água não é plana, havendo normalmente ondas.
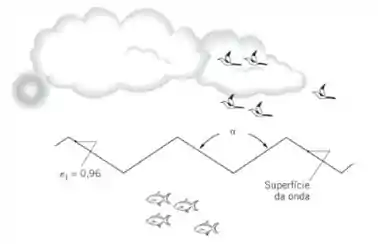
- Supondo que a geometria das ondas possa ser aproximada de perto como bidimensional e como mostrada na figura, determine a emissividade efetiva da superfície da água, como definida no Problema 13.43, para α = 3π/4.
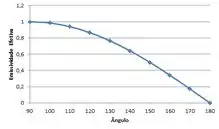
- Calcule e represente graficamente a emissividade efetiva da superfície da água, normalizada pela emissividade hemisférica da água , na faixa de π/2 ≤ α ≤ π.
Passo 1
Animados para seguir que eu sei, não é?
Vamos melhorar este desenho:
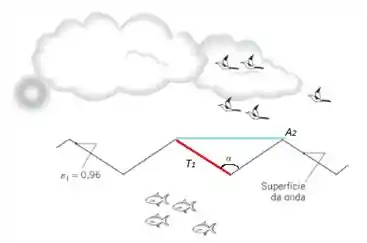
Para a transferência de calor por radiação podemos usar:
Reescrevendo o calor usando a emissividade efetiva:
Vamos ver o que temos?
A trigonometria nos ajuda a achar a área:
Sabendo que:
E usando a reciprocidade:
Agora tá fácil !! É só substituir:
Quando
Shoow !! Finalizamos a letra (a) !!
Passo 2
Na letra (b) nós queremos achar variando . Para isso basta substituir cada ângulo na equação:
Usando um software para gerarmos nossos dados:
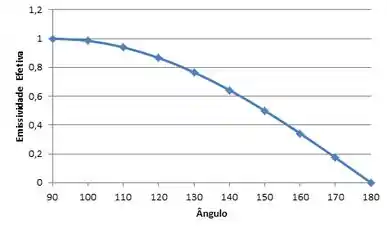
E é isso aí galerinhaaa !!