Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 45

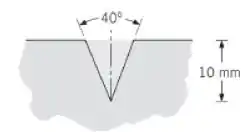
Considere uma longa fenda em forma de V, com profundidade de 10 mm, usinada em um bloco mantido a 1000 K. Se as superfícies da fenda são difusas e cinzas com uma emissividade de 0,6, determine o fluxo radiante que deixa a fenda para sua vizinhança. Determine também a emissividade efetiva da cavidade, como definida no Problema 13.43.

Passo 1

Faaaaala aí galerinha !! Animados?

Então booora !!

O problema nos pediu para achar o fluxo radiante que deixa a fenda (1) para sua vizinhança (2), tranquilo ?!

Para achar o fluxo radiante vamos usar a relação que já estamos carecas de saber:

q 12 = σ T 1 4 - T 2 4 1 - ε 1 ε 1 A 1 + 1 A 1 F 12 + 1 - ε 2 ε 2 A 2

Assumindo para a superfície 2, a interfase aberta entre a fenda e o ambiente:

ε 2 = 1

T 2 = 0   K

Então:

q 12 = σ T 1 4 - T 2 4 1 - ε 1 ε 1 A 1 + 1 A 1 F 12

Para calcular o calor por unidade de área que deixa a fenda:

q ' 12 = q 12 A 2

Então:

q ' 12 = σ T 1 4 - T 2 4 1 - ε 1 ε 1 A 1 + 1 A 1 F 12 A 2 = σ T 1 4 - T 2 4 1 - ε 1 ε 1   A 2 A 1 + A 2 A 1 F 12

q ' 12 = σ T 1 4 - T 2 4 A 2 A 1 1 - ε 1 ε 1   + 1 F 12

Agora vamos começar a avaliar o que temos, ok?

T 1 = 1000   K

ε 1 = 0,6

F 2 1 = 1

Para calcular a área nós vamos pedir ajuda pra trigonometria:

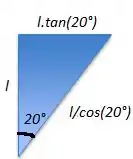
Então:

A 1 = 2 l cos ⁡ 20 °

A 2 = 2 l . tan ⁡ 20 °

Com isso nós podemos calcular o fator forma, basta usar a reciprocidade:

A 1 F 12 = A 2 F 21

F 12 = 2 l . tan ⁡ 20 ° 2 l cos ⁡ 20 ° 1 = tan ⁡ 20 ° cos ⁡ 20 ° = 0,342

Substituindo:

q ' 12 = 5,67 × 10 - 8 1000 4 - 0 4 0,342 1 - 0,6 0,6   + 1 0,342

q ' 12 = 46172,6 W m 2  

Shoow !! Achamos o fluxo radiante que deixa a fenda !! Mas não acabamos !!

Passo 2

O problema nos pediu para acharmos também a emissividade efetiva da cavidade !!

Vamos lembrar que fórmula usar?

q ' 12 = ε e f E b , 1

Lembrando que:

E b , 1 = σ T 1 4

Então:

q ' 12 = ε e f σ T 1 4

ε e f = q ' 12 σ T 1 4

Substituindo:

ε e f = 46172,6 5,67 × 10 - 8 1000 4

ε e f = 0,8144

E é isso galerinhaaa !! Finalizamos mais umaa !!

Resposta

  1. q ' 12 = 46172,6 W m 2
  2. ε e f = 0 , 8144
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

101 - Um secador é moldado como um duto semicilíndrico longo de diâmetro de 1,5m .A base do secador é ocupada por materiais encharcados com água e mantidos e mantida a uma temperatura de 370K com uma
103 - Considere dois discos paralelos coaxiais de diâmetros a e b , mostrado na Fig. P13-103.Para essa geometria, o fator de forma do disco menor para o disco maior pode ser calculado por F = 0,5 B A
112 - Um coletor solar é constituído por um tubo de cobre horizontal de 5c m de diâmetro externo envolto por um tubo de vidro fino concêntrico de 12c m de diâmetro.A água é aquecida à medida que flui
104 - Um grande número de longos tubos, cada um com diâmetro D , é colocado paralelo um ao outro e com distância centro a centro s .Uma vez que todos os tubos são geometricamente semelhantes e estão n
113 - Dois discos paralelos concêntricos, 20c m e 40c m de diâmetro são separados por uma distância de 10c m .O disco menor ( ε = 0,80 ) se encontra a uma temperatura de 300° C .O disco maior ε = 0,60