Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 127

Considere o campo de escoamento formado pela combinação de um escoamento uniforme no sentido positivo de x e uma fonte localizada na origem. Seja U = 30   m / s e q = 150   m 2 / s . Trace um gráfico da razão entre a velocidade local e a velocidade da corrente livre v e r s u s   θ , ao longo da linha de corrente de estagnação. Localize os pontos sobre a linha de corrente de estagnação onde a velocidade atinge seu valor máximo. Determine a pressão manométrica ali, considerando a massa específica do fluido igual a 1,2   k g / m 3 .

Passo 1

Pela Tabela 6.2: Escoamentos Planos Elementares obtemos a função de fluxo para um fluxo uniforme:

Ψ u n i f o r m e x , y = U y

Sendo:

y = r   s e n   θ .

Temos:

Ψ u n i f o r m e r , y = U r   s e n   θ

Determinando pela Tabela 6.2: Escoamentos Planos Elementares a função de fluxo para um fluxo de fonte localizado na origem:

ψ o r i g e m r , θ = q 2 π θ

Obtendo a função de fluxo para o fluxo combinado:

ψ = ψ u n i f o r m e + ψ o r i g e m

Substituindo:

ψ = U r   s e n   θ + q 2 π θ

Passo 2

Determinando a componente da velocidade na direção  x :

u = u u n i f o r m e + u o r i g e m

Sendo:

u u n i f o r m e = U ;

u o r i g e m = V r cos ⁡ θ ;

V r = q 2 π r ;

cos ⁡ θ = x r .

Temos:

u = U + V r cos ⁡ θ

u = U + q 2 π r ⋅ x r

u = U + q x 2 π r 2

Passo 3

Determinando a componente da velocidade na direção  y :

v = v u n i f o r m e + v o r i g e m

Sendo:

v u n i f o r m e = 0 ;

v o r i g e m = V r sen ⁡ θ ;

V r = q 2 π r ;

s e n   θ = y r .

Temos:

v = 0 + V r sen ⁡ θ

v = q 2 π r ⋅ y r

v = q y 2 π r 2

Passo 4

Determinando a função do campo de velocidade do fluxo:

V → = u i ^ + v j ^

Substituindo as equações obtidas nos Passos 2 e 3:

V → = U + q x 2 π r 2 i ^ + q y 2 π r 2 j ^

Calculando o módulo da velocidade do fluxo:

V 2 = u 2 + v 2

V 2 = U + q x 2 π r 2 2 + q y 2 π r 2 2

V 2 = U 2 + U q x π r 2 + q x 2 π r 2 2 + q y 2 π r 2 2

Sendo;

x = r cos ⁡ θ ;

y = r   s e n   θ .

Temos:

V 2 = U 2 + U q ⋅ r cos ⁡ θ π r 2 + q ⋅ r cos ⁡ θ 2 π r 2 2 + q ⋅ r   s e n   θ 2 π r 2 2

V 2 = U 2 + U q cos ⁡ θ π r + q ⋅ r cos ⁡ θ 2 π r 2 2 + q ⋅ r   s e n   θ 2 π r 2 2

V 2 = U 2 + U q cos ⁡ θ π r + q 2 π r 2  

Passo 5

Determinando os pontos de estagnação.

Com:

V → = 0

Temos:

U + q x 2 π r 2 i ^ + q y 2 π r 2 j ^ = 0

Determinando os pontos de estagnação igualando a componente y  a zero:

q y 2 π x 2 + y 2 j ^ = 0

y = 0

Determinando os pontos de estagnação igualando a componente x  a zero:

U + q x 2 π x 2 + y 2 î = 0

Sendo:

y = 0 .

Temos:

U + q x 2 π x 2 î = 0

U = - q 2 π x

x = - q 2 π U

Sendo:

U = 30   m / s ;

q = 150   m 2 / s .

Temos:

x = - 150 2 π ⋅ 30

x = - 0,796   m

Passo 6

Calculando o ângulo de inclinação da partícula com o eixo x  no ponto de estagnação:

θ = tan - 1 ⁡ y x

Sendo:

y = 0 ;

x = - 0,796   m .

Temos:

θ = tan - 1 ⁡ 0 - 0 , 7 96

θ = 180 ° = π   r a d

Calculando a função de fluxo no ponto de estagnação:

ψ = U r   s e n   θ + q 2 π θ

Substituindo os dados:

ψ = U ⋅ r   s e n   π + q 2 π ⋅ π

ψ = q 2

Calculando o raio da linha de estagnação:

ψ = U r   s e n   θ + q 2 π θ

Substituindo ψ :

q 2 = U r   s e n   θ + q 2 π θ

r = q π - θ 2 π U   s e n   θ

Passo 7

Determinando a relação entre  V  e  U :

V 2 = U 2 + U q cos ⁡ θ π r + q 2 π r 2

Substituindo r :

V 2 = U 2 + U q cos ⁡ θ π ⋅ q π - θ 2 π U   s e n   θ   + q 2 π q π - θ 2 π U   s e n   θ 2

V U = 1 + s e n   2 θ π - θ + s e n 2   θ π - θ 2

Para 0 ≤ θ ≤ 180 ° , temos:

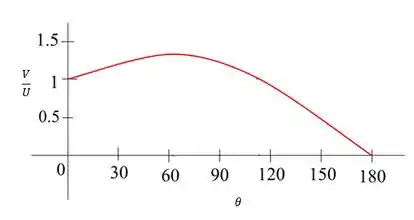
Temos que o máximo é atingido em 63 ° ou 7 π / 20   r a d .

Calculando o valor máximo de V / U :

V U = 1 + s e n   2 θ π - θ + s e n 2   θ π - θ 2

Sendo:

θ = 7 π / 20 .

Temos:

V U = 1 + s e n   2 ⋅ 7 π / 20 π - 7 π / 20 + s e n 2   7 π / 20 π - 7 π / 20 2

V U = 1,26

Calculando o raio da linha de estagnação:

r = q π - θ 2 π U   s e n   θ

Substituindo os dados:

r = 150 ⋅ π - 7 π / 20 2 π ⋅ 30 ⋅ s e n   ( 7 π / 20 )

r = 1,82   m

Passo 8

Calculando a pressão manométrica com a equação de Bernoulli:

p ∞ ρ + U 2 2 = p ρ + V m á x 2 2

p - p ∞ = p m a n = ρ U 2 2 1 - V m á x 2 U 2

Sendo:

ρ = 1,2   k g / m 3 ;

U = 30   m / s ;

V U = 1,26   m / s .

Temos:

p m a n = 1,2 ⋅ 30 2 2 1 - 1,26 2

p m a n = - 317,3   P a

Resposta

θ = 63 °

r = 1,82   m

p m a n = - 317,3   P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma fonte pontual com vazão volumétrica Q = 30m 3 / s é imersa em uma corrente uniforme com 4 m/s de velocidade. Resulta um semicorpo de Rankine de revolução. Calcule (a) a distância da fonte ao ponto
O corpo de revolução de Rankine na figura abaixo tem 60 cm de comprimento e 30 cm de diâmetro. Quando imerso no túnel hidrodinâmico de baixa pressão como mostrado, a cavitação pode aparecer no ponto A
Modifique o problema 8.50 da seguinte maneira: A saliência deve ser tal que U m á x = 1,5 U ∞ á . Encontre (a) a elevação h e (b) a altura Z da saliência.
Considere o ar escoando sobre um hemisfério assentado sobre uma superfície plana, como na figura a seguir. Se a pressão interna é p i , encontre uma expressão para a força de pressão sobre o hemisféri
Se ϕ ( r , θ ) no escoamento com simetria axial é definida pela equação 8.85 e as coordenadas são dadas na figura 8.29, determine qual a equação diferencial parcial que ϕ deve satisfazer.