Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 23

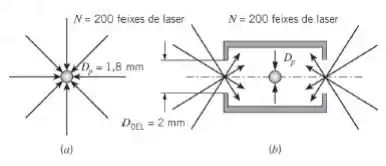
Propõe-se que as temperaturas extremamente altas necessárias para disparar a fusão nuclear sejam geradas pela irradiação com laser de uma pequena partícula de deotério e trítio com diâmetro Dp = 1,8 mm.

  1. Determine a temperatura do combustível máxima que pode ser atingida pela irradiação da partícula com 200 lasers, cada um produzindo uma potência de P = 500 W. A partícula tem uma absortividade α = 0,3 e emissividade ε = 0,8.
  2. A partícula é posicionada no interior de um recinto cilíndrico. Dois orifícios para entrada dos lasers estão localizados em cada extremidade do recipiente e têm um diâmetro de DOEL = 2 mm. Determine a temperatura máxima que pode ser gerada no interior do recipiente.

Passo 1

Fala aí! Partiu resolver essa questãozinha juntos? Com certeza!!

A letra a pediu a temperatura máxima do combustível, beleza?

Podemos fazer um balanço de energia, dessa forma vamos ter:

E e n t = E s a i

α   .   N   .   P = π   .   D p 2   .   ε   .   σ   .   T p 4

T p = α   .   N   .   P π   .   D p 2   .   ε   .   σ 1 / 4

T p = 0,3   .   200   .   500 π   .   1,8   .   10 - 3 2   .   0,8   .   5,67   .   10 - 8 1 / 4

T p = 15970   K

Show de bola! Agora só falta a letra b…

Passo 2

Na letra b, o enunciado quer a temperatura máxima gerada dentro do recipiente… Vamos seguir o mesmo procedimento, fazer o balanço de energia:

E e n t = E s a i

N   .   P = 2   .   π   .   D L E H 2 4 .   σ   .   T e 4

T e = 2   .   N   .   P π   .   D L E H 2   .   σ 1 / 4

T e = 2   .   200   .   500 π   .   2   .   10 - 3 2   .   5,67   .   10 - 8 1 / 4

T e = 23020   K = T p

Prontinho! Arrasamos!

Resposta

  1. T p = 15970   K

  2. T p = 23020   K
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o Prob. 12–36 para uma esfera de 4m de diâmetro.
Uma pequena superfície de área A 1 =7c m 2 emite radiação como um corpo negro a T 1 =800K . Parte da radiação emitida por A 1 atinge outra pequena superfície da área A 2 =7c m 2 , orientada como
Uma pequena superfície de área A 1 =3c m 2 emite radiação como um corpo negro com poder emissivo total de E b =5,67×10 4W / m 2 . Parte da radiação emitida porA 1 atinge outra pequena superfície da
Considere que a intensidade da radiação solar incidente sobre a superfície terrestre pode ser expressa como I i = 100 cos ⁡ θ , onde I i tem as unidades de W / m 2 . s r . Determine o valor de pico da
Uma pequena superfície de área emite radiação como um corpo negro a T 1 = 1000K . Um detector de radiação ( A 2 ) é colocado à direção normal de visualização da superfície A 1 , a distância L, como mo