Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 14

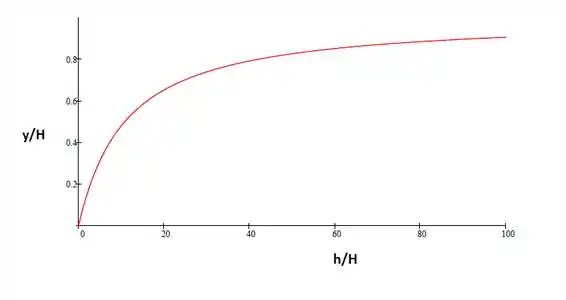
Um recipiente cilíndrico é imerso vagarosamente de “boca para baixo” em uma piscina. O ar aprisionado no recipiente é comprimido isotermicamente enquanto a pressão hidrostática aumenta. Desenvolva uma expressão para a altura de água, y, dentro do recipiente, em termos da altura do recipiente, H, e da profundidade de imersão, h. Trace um gráfico de y/h em função de h/H.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiramente, sabemos que:

d ρ d h = ρ g

p V = N R T

Primeiro, aplicamos a equação do gás ideal para a pressão do ar no recipiente com temperatura constante:

p V = p a π 4 D 2 H = ρ π 4 D 2 H - y → p a H = p H - y

Agora, examinamos a equação da pressão hidrostática para a pressão exercida pela água. Como ρ é constante, integramos:

p - p a = ρ g h - y

Como o copo está submerso a uma profundidade de h, essas pressões devem ser iguais, logo:

p a H = p a + ρ g h - y H - y = p a H - p a y + ρ g h - y H - y

Expandindo o lado direito desta expressão e isolando o y :

y = p a ρ g + h + H - p a ρ g + h + H 2 - 4 h H 2

Agora, basta dividir ambos os lados por H :

y H = p a ρ g H + h H + 1 - p a ρ g H + h H + 1 2 - 4 h H 2

A forma exata dessa curva dependerá da altura do copo. O gráfico abaixo foi gerado assumindo:

p a = 101,3 k P a

H = 1 m

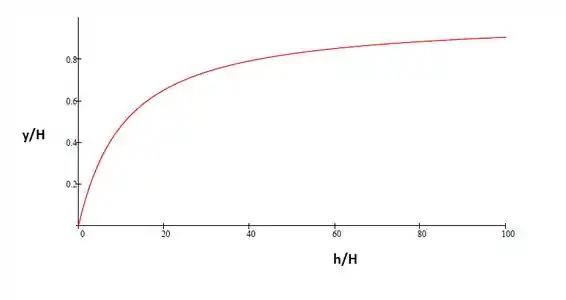
Resposta

y H = p a ρ g H + h H + 1 - p a ρ g H + h H + 1 2 - 4 h H 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o tanque do Problema 3.29 for selecionado hermeticamente e a água para drenada lentamente pelo fundo, determine um deflexão, l , após o sistema ter atingido o equilíbrio.
No nível do solo em Denver, Colorado, a pressão e a temperatura atmosféricas são respectivamente 83,2 kPa e 25ºC. Calcule a pressão em Pike’s Peak em uma elevação de 2690 m acima da cidade, consideran
Uma porta de acesso, de 1 m de largura e 1,5 m de altura, está localizada em uma parede plana e vertical de um tanque de água. A porta é articulada ao longo da borda superior que está 1 m abaixo da su
Um barômetro contém acidentalmente 165 mm de água no topo da coluna de mercúrio (nesse caso, existe vapor d’água em vez de vácuo no topo do barômetro). Em um dia em que a temperatura ambiente é 21ºC,
Considerar um tubo de pequeno diâmetro e extremidades abertas inserido na interface entre dois cortes imiscíveis de massas específicos diferentes. Deduza uma expressão para a diferença de nível Δh ent