Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 44

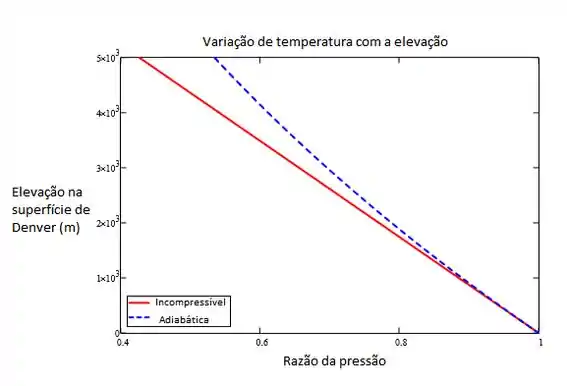
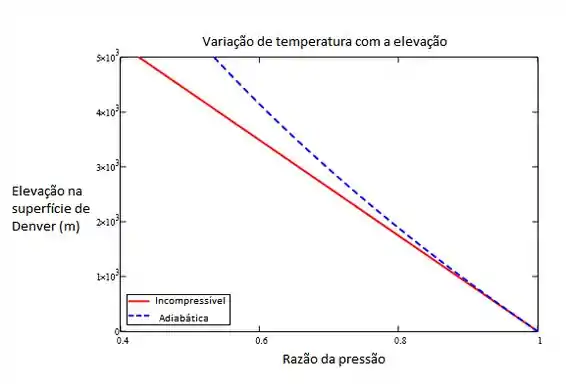
No nível do solo em Denver, Colorado, a pressão e a temperatura atmosféricas são respectivamente 83,2 kPa e 25ºC. Calcule a pressão em Pike’s Peak em uma elevação de 2690 m acima da cidade, considerando uma atmosfera (a) incompressível e (b) adiabática. Trace um gráfico da razão entre a pressão e a pressão na superfície de Denver como uma função da elevação para ambos os casos.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiramente, sabemos que:

d p d z = - ρ g

Em uma atmosfera imcompressível, essa expressão pode ser usada como:

p - p 0 = - ∫ 0 z ρ d d z

Resolvendo:

p = p 0 - ρ 0 g z = p 0 1 - g z R T 0 → e q u a ç ã o   1

Quando z = 2690 m ,   a pressão será:

p = 57,5 k P a

Passo 2

Já para uma amosfera adiabática:

p ρ k = c t e

ρ = ρ 0 p p 0 1 k

Logo, substituindo:

d p d z = - ρ g

d p = - ρ 0 p p 0 1 k g d z

Separando a equação diferencial:

1 p 1 k d p = ρ 0 g p 0 1 k d z

Logo, integrando e isolando p p 0 :

p p 0 = 1 - k - 1 k g z R T 0 k k - 1 → e q u a ç ã o   2

Portanto, substituindo:

p = 60,2 k P a

Passo 3

Para o gráfico, basta plotar o comportamento das equações 1 e 2:

Resposta

  1. p = 57,5 k P a
  2. p = 60,2 k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A pressão sanguínea em geral é medida colocando-se um involucro cheio de ar e fechado equipado com um medidor manométrico de pressão ao redor da parte superior do braço de uma pessoa no nível do coraç
A pressão sanguínea máxima na parte superior do braço de uma pessoa saudável é de cerca de 120m m H g . Se um tubo vertical aberto para a atmosfera estiver conectado à veia do braço da pessoa, determi
Um experimento simples há muito tempo é usado para demonstrar como a pressão negativa evita que a água seja derramada para fora de um copo invertido. Um copo completamente cheio com água e coberto com
Considere um manômetro de fluido duplo preso a um tubo de ar mostrado na Figura P3-40. Se a gravidade específica de um fluido for 13,55, determine a gravidade específica do outro fluido para a pressão
Considere o sistema mostrado na Figura P3 – 42. Se uma alteração de 0,7k P a na pressão do ar fizer com que a interface entre a água salgada e o mercúrio da coluna da direita caia em 5m m no nível da