70 – Reconsidere o Prob. 2-69. Usando a relação obtida para a variação de temperatura no contêiner, trace a temperatura como função do raio no intervalo de a e discuta os resultados. Use EES (ou outro programa).

Escreva a equação geral de condução de calor na direção radial, estado estacionário sem geração interna de calor.

Integre a equação diferencial acima,

Aqui é a constante de integração.

Novamente, integre a equação acima,

Aqui, é a constante de integração.

Aplique a segunda condição de contorno para encontrar o valor constante  da equação (1). Assumindo que:

Aplique a primeira condição de contorno para encontrar o valor constante  da equação (2). Logo, temos que e

Agora substitua esse valor de e o valor de na equação (2).

Substituindo pelos valores conhecidos, temos:

Portanto, a distribuição de temperatura no recipiente é 

Agora tabule os valores da temperatura em diferentes valores, do raio interno até , como mostrado abaixo:

Agora plote o gráfico que mostra a variação de temperatura em função do raio .

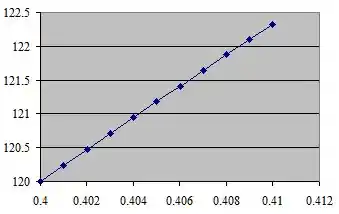
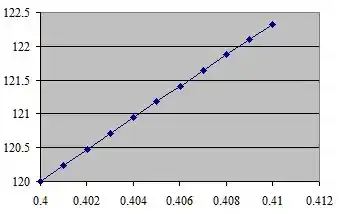
Percebemos que com o aumento do raio, temos um aumento da temperatura.