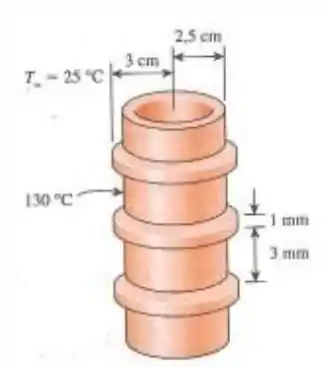
O vapor de água em um sistema de aquecimento flui através de tubos cujo diâmetro externo é de 5 cm e cujas paredes são mantidas a uma temperatura de 130°C. Aletas circulares de liga de alumínio 2024-T6 de diâmetro externo de 6 cm e espessura constante de 1 mm são fixadas ao tubo. O espaço entre as aletas é de 3 mm e, portanto, existem 250 aletas por metro de comprimento do tubo. O calor é transferido para o ar circundante a , com um coeficiente de transferência de calor de . Determine o aumento da transferência de calor a partir do tubo por metro de seu comprimento, como resultado da adição de aletas.

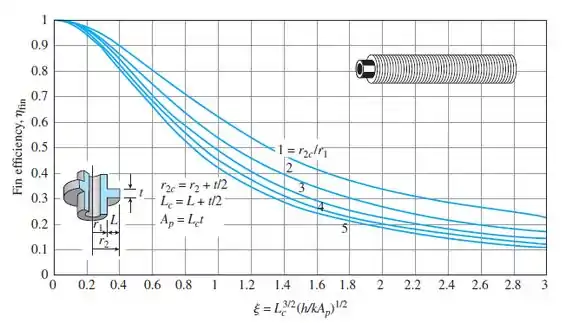
E para achar a eficiência vamos usar o gráfico que foi dado no livro:

Vamos precisar achar a razão e

Começando pela razão e lembrando que:

Então:

Substituindo:

E quanto ao

Se:

Então:

Em função do raio:

Substituindo:

Analisando o gráfico para e , a eficiência será próxima de 0,97.

Então:

Agora temos tudo o que precisamos nós vamos lançar nossos dados na fórmula do passo 1:

Como a variação em graus Celsius e em kelvin é a mesma:

Legal, achamos a troca de calor que ocorre a partir de uma aleta, mas nós sabemos que na verdade existem 250 aletas iguais a esta.

Então na verdade a troca de calor será dada por:

Agora o que nós precisamos é achar qual a troca de calor para a superfície sem aletas.

E para isso nós vamos usar:

A área aqui será calculada em função do raio do tubo, uma vez que estamos desconsiderando a aleta:

Substituindo:

Achando o calor:

Este é o valor para uma superfície sem uma aleta, só que nós não temos uma aleta, certo?

Agora temos tudo o que precisamos para achar a variação:

E fim !!