Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 1.Problemas - Ex. 44
Rejeitos radiativos são estocados em recipientes cilíndricos longos e com paredes finas. Os rejeitos geram energia térmica de forma não-uniforme, de acordo com a relação onde é a taxa local de geração de energia por unidade de volume, é uma constante e é o raio do recipiente. Condições de regime estacionário são mantidas pela submersão do recipiente em um líquido que está a fornece um coeficiente de transferência de calor por convecção uniforme e igual a h.
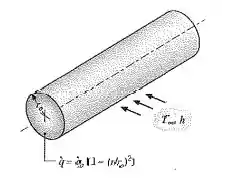
Obtenha uma expressão para a taxa total na qual a energia é gerada por unidade de comprimento do recipiente. Use esse resultado para obter uma expressão para a temperatura da parede do recipiente.
Passo 1
E ai meus amores nessa questãozinha “Pegue o que puder, sem nada a devolver” okay?
Começaremos escrevendo a relação para a taxa de geração de energia
Onde é a taxa local de geração de energia por unidade de volume e e a mudança de volume
Vamos substituir essa formula seguinte por
E por .
Passo 2
Fazendo as devidas substituições
Onde
é o comprimento unitário do contêiner
é a taxa de geração de energia por unidade de comprimento
é a constante
é o raio do contêiner
Portanto, a expressão para a taxa total na qual a energia é gerada em uma unidade de comprimento do recipiente é de
Passo 3
Vamos agora escrever a relação para a taxa de calor por convecção por unidade de comprimento
A taxa na qual a energia é gerada em uma unidade de comprimento do recipiente é balanceada pela taxa de calor por convecção por unidade de comprimento de acordo com o balanço de energia para uma superfície de controle de um recipiente.
Portanto, a expressão para a temperatura da parede do recipiente é
Depois dessa questão, “Ninguém se mexe” Meu cérebro caiu.”
Haha bora pra proximaaaa
Resposta
Portanto, a expressão para a taxa total na qual a energia é gerada em uma unidade de comprimento do recipiente é de
Portanto, a expressão para a temperatura da parede do recipiente é