Desenvolva a equação da difusão térmica, Equação 2.24, em coordenadas cilíndricas, a partir do volume de controle diferencial mostrado na Figura 2.12.
Passo 1
Selvaaaaaaaaaa galerinha, isso mesmo selva haha, tudo certinho??
“Hulk esmaga”, Bora esmagar essa questãozinha comigo?

Vamos considerar um volume de controle diferencial como mostra a figura a seguir
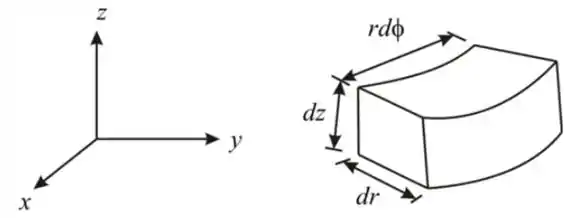
Passo 2
Vamos aplicar o balanço de energia ao sistema
Onde, a entrada de energia é
A saída de energia é
A taxa de geração de energia térmica é
E a taxa de armazenamento de energia é
Considerando a expressão para o fluxo de calor, teremos
Onde, as taxas de calor por condução na direção da face de entrada do elemento são respectivamente.
Para a saída de calor, teremos a seguinte expressão
Onde, as taxas de calor por condução na direção da face de entrada do elemento são respectivamente.
Passo 3
Vamos considerar a expressão para a taxa de geração de energia térmica
Considerando a expressão para o armazenamento de energia
Agora vamos substituir as expressões que encontramos no passo 2, show?
Passo 4
Agora iremos escrever a taxa de calor por condução na direção de r em um material isotrópico pela lei de Fourier
Onde a área da face na direção de r é e o comprimento do volume elementar nas direções , são .
Vamos escrever a taxa de calor por condução na direção , em um material isotrópico pela lei de Fourier
Vamos escrever a taxa de calor por condução na direção de z em um material isotrópico pela lei de Fourier
Onde, a área da face na direção de z é .
Passo 5
Vamos escrever a expressão para o volume do elemento diferencial
Usaremos a expansão da série de Taylor na expressão a seguir, e desprezaremos os termos superiores.
Manipulando essa outra expressão, teremos
Passo 6
Vamos diferenciar as seguintes equações, para obter as derivadas do fluxo de calor em diferentes direções.
Diferenciando
Passo 7
Agora pra finalizar o exercício iremos substituir essas 3 equações diferenciadas que encontramos na seguinte fórmula
Logo, vamos dividir essa expressão por
Sendo assim, a equação de difusão de calor com geração de calor em coordenadas cilíndricas foi derivada.
“OK, isso foi legal.”

Resposta
Resposta nos passos.