Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 2.Problemas - Ex. 50

Repita o Prob. 2 - 49 para u_m á x = 5 m // s .

Passo 1

A questão pede que a gente calcule a força de arrasto F que o fluido aplica sobre a superfície interna do tubo assim como a gente fez para o Prob. 2 - 49 . A água se movimenta através de um tubo e tenta empurrar a parede do tubo por meio do atrito. A figura abaixo mostra o valor de todas as variáveis do fluido que precisamos para encontrar F . Entender o que são essas variáveis é o primeiro passo para resolver essa questão!

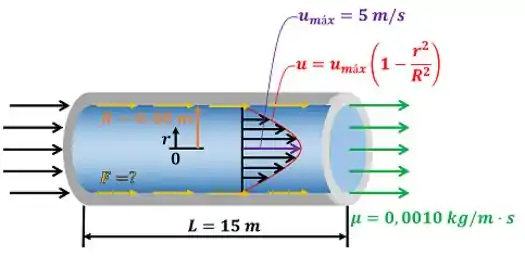
u é a velocidade do fluido na direção do comprimento do tubo. Ela varia com a distância r entre o ponto do fluido e o eixo do tubo. L é o comprimento do tubo. mu é a viscosidade dinâmica do fluido.

No próximo passo, vamos aprender a primeira etapa de cálculo de F .

Passo 2

Para calcular F precisamos primeiro calcular a tensão de cisalhamento tau que o fluido aplica sobre a superfície interna do fluido. Para calcular tau precisamos transformar a equação 2 - 29 do livro. Essa fórmula diz que:

tau = mu * (d u)/(d y)

Essa fórmula mostra que a tensão de cisalhamento tau é proporcional à taxa de variação da velocidade do fluido u em relação a coordenada y . No caso de um tubo cilíndrico, a coordenada y deve ser trocada pela coordenada r . Além disso, devemos acrescentar o sinal de menos na fórmula, porque o r e contado a partir do centro do eixo e não a partir da parede como é o caso da coordenada y . Isso quer dizer que y e r possuem sentidos opostos.

tau = - mu * (d u)/(d r)

Isso quer dizer que teremos que derivar u para encontrar tau .

Passo 3

Derivando u , encontramos:

(d u)/(d r) = (d)/(d r) (u_m á x (1 - (r^2)/(R^2))) ⟹ (d u)/(d r) = - u_m á x * (2 * r)/(R^2)

No entanto, nós não queremos o valor de tau em qualquer ponto. Nós queremos saber o valor de tau na parede do tubo. Ou seja, nós queremos saber o valor de tau , quando r = R . Por isso, temos que calcular (d u)/(d r) onde r é igual a R .

Substituindo r por R na equação acima encontramos:

(d u)/(d r) = - u_m á x * (2 * r)/(R^2) ⟹ (d u)/(d r) = - u_m á x * (2 * R)/(R^2) ⟹ (d u)/(d r) = - u_m á x * (2)/(R)

Substituindo essa fórmula na equação de tau , achamos:

tau = - mu * (d u)/(d r) ⟹ tau = - mu * (- u_m á x * (2)/(R)) ⟹ tau = mu * u_m á x * (2)/(R)

Passo 4

A tensão de cisalhamento tau que a gente encontrou é a força F por unidade de área. Para encontrar F , temos que multiplicar tau pela área A da superfície do tubo de comprimento L . O valor dessa área A é igual ao perímetro interno do tubo (2 * pi * R) multiplicado pelo seu comprimento L .

F = tau * A ⟹ F = tau * 2 * pi * R * L ⟹ F = mu * u_m á x * (2)/(R) * 2 * pi * R * L

F = u_m á x * mu * 4 * pi * L

Passo 5

Com essa fórmula podemos achar o valor de F para R = 0,08 m , L = 15 m , u_m á x = 5 m // s , e mu = 0,0010 k g // m * s . Podemos encontrar o valor de F , substituindo esses dados na fórmula que encontramos.

F = u_m á x * mu * 4 * pi * L ⟹ F = 5 * 0,0010 * 4 * pi * 15 ⟹ F=0,942N

Resposta

F = 0 , 942 N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Deduza os seguintes fatores de conversão:Converta um calor específico de 4,18 k J / k g K para B t u / l b m R . Converta uma velocidade de 30 m / s para m p h . Converta um volume de 5,0 L para in³
O livre caminho médio λ de uma molécula de gás é a distância média que ela percorre antes de colidir com outra molécula. Ele é dado por: γ = C m ρ d 2 Em que m e d são a massa da molécula e o diâmetro
Uma determinada bomba tem sua equação característica de desempenho, relacionando a altura manométrica H com a vazão Q, dada por H (m) = 0,46 – 9,57 × 10 - 7 [Q (Lit/min)]². Quais são as unidades dos c
Um recipiente pesa 15,5 N quando vazio. Quando cheio com água a 32°C, a massa do recipiente e do seu conteúdo é de 36,5 kg. Determine o peso da água no recipiente, e o seu volume em pés cúbicos, usand
Calcule a massa específica do ar­padrão a partir da equação de estado do gás ideal. Estime a incerteza experimental na massa específica calculada para a condição­padrão (101,3 kPa e 15°C) se a incerte