Enunciado
Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 76
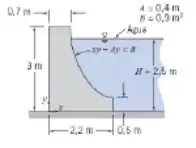
Uma represa deve ser construída usando a seção transversal mostrada. Suponha que a largura da represa seja w = 50 m. Para uma altura de água H = 2,5 m calcule o módulo e a linha de ação da força vertical da água sobre a face da represa. É possível que a força da água derrube essa represa? Sob quais circunstâncias?
Passo 1
Nessa questão temos uma barragem com seção transversal. Vamos encontrar magnitude e linha de ação do componente de força vertical na barragem e se é possível a água derrubar a barragem.
Para resolução, aplicaremos as equações hidrostáticas a seguir:
, pressão hidrostática
, equilíbrio de rotação
, força hidrostática vertical
, momento de força vertical
, momento de força horizontal
Como todo problema da MecFlu, fazemos as seguintes considerações: fluido estático e incompressível; pressão atmosférica atua na superfície livre da água e fora da barragem.
Passo 2
Começamos integrando a equação da pressão hidrostática na fórmula da força vertical:
A partir da definição do contorno da barragem:
Então:
E,
Na equação da força:
Substituindo valores:
Passo 3
Para encontramos a linha de força, temos:
Onde , então:
Resolvendo a integral:
Para determinar se a água pode ou não derrubar a barragem, precisamos da força horizontal e de sua linha de ação:
Substituindo valores:
Para a linha de ação,
Onde , e .
Calculando o momento:
O sinal negativo indica que o momento se dá no sentido horário. Como o peso da barragem também contribui para a direita do momento em relação a origem, esses dois momentos não devem fazer com que a barragem tombe para a esquerda. Portanto, a água não derruba a barragem.