Enunciado
Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 66
A comporta mostrada na figura é articulada em H. A comporta tem 3 m de largura em um plano normal ao diagrama mostrado. Calcule a força requerida em A para manter a comporta fechada.
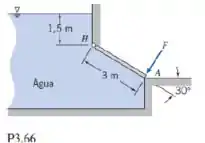
Passo 1
Nesse problema temos a geometria do portão e devemos encontrar a força necessária em para manter o portão fechado. Algumas das equações básicas que temos são:
Como todo problema da mecânica, temos que fazer algumas considerações: líquido estático; densidade constante; sem atrito na dobradiça.
Para um fluido incompressível , em que é a pressão manométrica e é medido para baixo.
A força hidrostática no portão é a de um retângulo de tamanho e largura .
Passo 2
Assim, temos:
Substituindo os dados temos:
Para acharmos a localização dessa força, fazemos:
Substituindo na fórmula,
Então, .
Passo 3
Calculando agora o momento sobre a dobradiça:
Então, a força requerida em A para manter a comporta fechada é .