Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 53

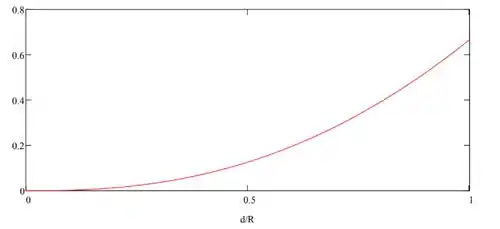
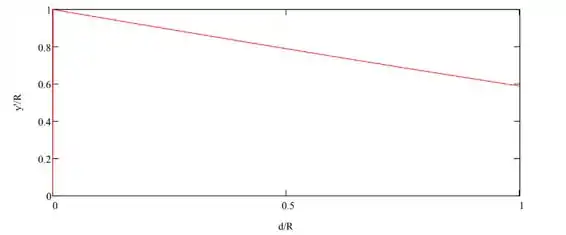
Considere um recipiente semicilíndrico de raio R e comprimento L. Desenvolva expressões gerais para o módulo e a linha de ação da força hidrostática em uma extremidade, se o recipiente estiver parcialmente cheio com água e aberto para a atmosfera. Plote os resultados (na forma adimensional) para a faixa de profundidade da água de 0 ≤ d/R ≤ 1.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiro, vamos integrar a equação da pressão. Todavia, temos que esboçar o DCL , que é da seguinte forma:

p = ρ g h h = y - ( R - d )

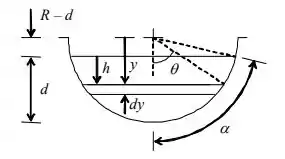
Então:

p = ρ g y - R - d = p g R y R - 1 - d R

Expressando em termos de θ , temos:

p = ρ g R ( cos ⁡ θ - cos ⁡ α )

d A = w   d y = 2 R sin ⁡ θ d y

y = - R sin ⁡ θ   d θ

Substituindo na equação da força hidrostática:

F R = ∫ R - d R p w   d y = ∫ α 0 ρ g R cos ⁡ θ - cos ⁡ α 2 R sin ⁡ θ ( - R sin ⁡ θ )   d θ F R ρ g R 3 = 2 sin 3 ⁡ α 3 - cos ⁡ α α 2 - sin ⁡ α cos ⁡ α 2

Passo 2

Agora, para encontrarmos a linha de ação da força, temos:

y ' F R = ∫ R - d R y p w   d y = ∫ α 0 R cos ⁡ θ ρ g R cos ⁡ θ - R sin ⁡ θ   d θ y ' R = 1 8 α - sin ⁡ 4 α 4 - cos ⁡ α sin 3 ⁡ α 3   sin 3 ⁡ α 3 - cos ⁡ α α 2 - sin ⁡ α cos ⁡ α 2

Com isso, nossos gráficos ficam assim:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma portinhola triangular de acesso deve ser projetada para ser colocada na lateral de uma forma contendo concreto líquido. Usando as coordenadas e dimensões mostradas, determine a força resultante qu
Uma comporta de vertedouro, com a forma de um arco circular, tem w metros de largura. Determine o módulo e a linha de ação da componente vertical da força devida a todos os fluidos atuando sobre a com
Concreto líquido é despejado na forma mostrada ( R=0,313m ). A forma tem largura w=4,25m normal ao diagrama. Calcule o módulo da força vertical exercida sobre a forma pelo concreto e especifique sua l
A comporta mostrada na figura é articulada em H. A comporta tem 3 m de largura em um plano normal ao diagrama mostrado. Calcule a força requerida em A para manter a comporta fechada.
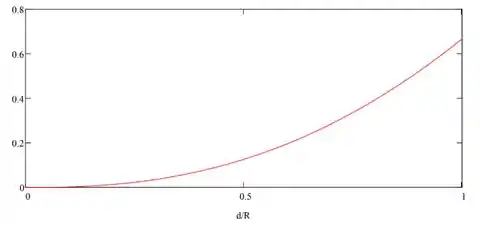
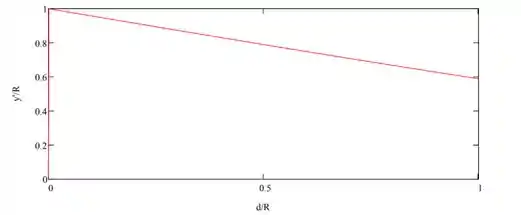
Um tanque aberto está cheio com água na profundidade indicada. A pressão atmosférica atua sobre todas as superfícies externas do tanque. Determine o módulo e a linha de ação da componente vertical da