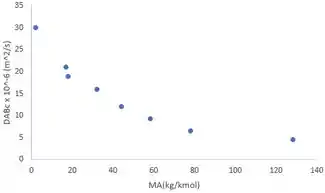
Represente graficamente a difusividade mássica, D A B , versus a massa molar da Substância A, sendo a Substância B ar a p=1,5a t m e T=320K . A Substância A é cada uma das 8 primeiras entradas na Tabela A.8. Seu gráfico está consistente em relação à teoria cinética? Consulte varias fontes, incluindo a Tabela A.4 e o Exemplo 6.2 para obter os valores das massas molares.

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 14.Problemas - Ex. 6

Represente graficamente a difusividade mássica, , versus a massa molar da Substância A, sendo a Substância B ar a e . A Substância A é cada uma das primeiras entradas na Tabela A.8. Seu gráfico está consistente em relação à teoria cinética? Consulte varias fontes, incluindo a Tabela A.4 e o Exemplo 6.2 para obter os valores das massas molares.

Passo 1

Nessa questão nós temos a pressão e temperatura e as substâncias A e B. A partir disso vamos encontrar o gráfico de versus para , , , , , acetona, benzeno e naftaleno no ar.

Passo 2

Para resolver essa questão vamos assumir mistura de gás ideal. Os valores de difusividade mássica devem ser corrigidos para levar em consideração a dependência de temperatura e pressão.

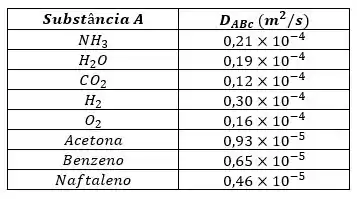
Na Tabela A.8, e a difusividade mássica corrigida para são:

Passo 3

Repetir o cálculo para as outras substâncias temos,

A seguir, é apresentado um gráfico das difusividades de massa corrigidas versus o peso molecular da Substância A.

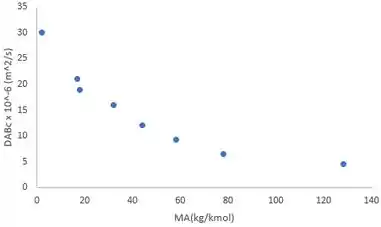
Segundo a teoria cinética, a difusividade de massa diminui com o aumento do peso molecular. Esse comportamento é prontamente evidente no gráfico e, portanto, a teoria cinética é consistente com os valores medidos.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um medicamento encontra-se no interior de um velho frasco farmacêutico de vidro. A boca está fechada com uma rolha de borracha que tem 20m m de altura, com 10m m de diâmetro na extremidade inferior, a

Uma gota esférica do líquido A, com raio r o , evapora para uma camada estagnada de um gás B. Deduza uma expressão para a taxa de evaporação da espécie A em termos da pressão de saturação de A, p A (

Uma fina membrana plástica é usada para separar hélio de uma corrente gasosa. Sob condições de regime estacionário, a concentração do hélio na membrana é conhecida como sendo 0,02 e 0,005k m o l / m 3

Partindo de um volume de controle diferencial, deduza a equação da difusão, em base molar, para a espécie A em um meio estacionário tridimensional (em coordenadas cartesianas), levando em consideração

Partindo de um volume de controle diferencial, deduza a equação da difusão, em base molar, para a espécie A em um meio estacionário esférico unidimensional, levando em conta a geração da espécie. Comp