Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 17

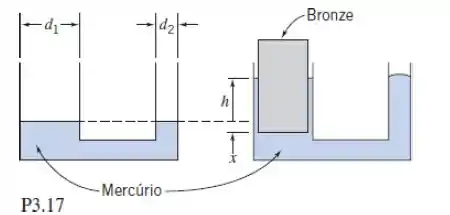
Um reservatório com dois tubos cilíndricos verticais de diâmetros d 1 =   39,5   m m e d 2   =   12,7   m m é parcialmente preenchido com mercúrio. O nível de equilíbrio do líquido é mostrado no diagrama da esquerda. Um objeto cilíndrico sólido, feito de latão, flutua no tubo maior conforme mostrado no diagrama da direita. O objeto tem diâmetro D   =   37,5   m m e altura H   =   76,2   m m . Calcule a pressão na superfície inferior necessária para fazer flutuar o objeto. Determine o novo nível de equilíbrio, h , do mercúrio com a presença do cilindro de metal.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Antes de tudo vamos anotar nossos dados, ok?

Temos:

  • Diâmetro do tubo menos: d 1 =   39,5   m m
  • Diâmetro do tubo maior: d 2   =   12,7   m m
  • Diâmetro do objeto: D   =   37,5   m m
  • Altura do objeto: H   =   76,2   m m

Mas existem dois parâmetros que são muito importantes pra gente e o enunciado não falou, então precisamos pegar eles no livro, ok?

Para o mercúrio:

S G H g = 13,55

Para o latão:

S G l a t ã o = 8,55

Bom, com nossos dados anotadinhos, sabemos que:

∑ F z = 0

Sabemos também que:

d p d z = - ρ   .     g

E que:

ρ = S G   .     ρ á g u a

Show! Então vamos às continhas!

Passo 2

Para equilíbrio, teremos:

∑ F z = p π 4 D 2 - ρ l a t ã o   g π 4   D 2 H = 0

Logo:

p = ρ l a t ã o   .     g   .     H = S G   .     ρ á g u a   .     g   .     H

Substituindo os nossos dados, vamos ficar com:

p = 8,55 ⋅ 1000 ⋅ 9,81 ⋅ 0,0762

A pressão será:

p = 6,39   k P a

Essa pressão deve ser gerada por uma coluna de mercúrio h   +   x de altura. Portanto:

p = ρ h g   .   g   .   h + x = S G h g   .     ρ á g u a   .     g   .   h + x = S G l a t ã o   .     ρ á g u a   .     g   .     H

Logo:

h + x = S G l a t ã o S G h g H

O valor de x pode ser encontrado ao se perceber que o volume de mercúrio no sistema permanece constante… Opa! Então ficaremos com:

π 4 D 2 x = π 4 d 1 2 - D 2 h + π 4 d 2 2 h

Isolando o x :

x = d 1 D 2 - 1 + d 2 D 2 h

Beleza! E se a gente substituir o x   para achar o h , vamos ficar com:

h = S G l a t ã o S G H g × D 2 d 1 2 + d 2 2 H

Substituindo os valores que temos:

h = 8,55 13,55 × 37,5 2 39,5 ² + 12,7 ² ⋅ 76,2

Sendo assim:

h = 39,3   m m

Prontinho!

Resposta

h = 39,3   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um recipiente cilíndrico é imerso vagarosamente de “boca para baixo” em uma piscina. O ar aprisionado no recipiente é comprimido isotermicamente enquanto a pressão hidrostática aumenta. Desenvolva uma
Compare uma altura devido à ação capilar da água exposta ao ar em um tubo circular de diâmetro D = 0,5 mm, e entre duas placas planas verticais infinitas com espaçamento a = 0,5 mm entre elas.
Duas placas de vidro verticais de 300 mm × 300 mm estão colocadas em um tanque aberto. Em uma das extremidades laterais, uma faixa entre placas de 0,1 mm e outra de 2 mm. Trace uma curva da altura da
Uma coluna de água de 50 mm de altura está em um tubo de vidro de 2,5 mm de diâmetro. Qual seria a altura da coluna se um tensão superficial fosse zero? Qual seria a altura da coluna em um tubo com 1,