Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 18
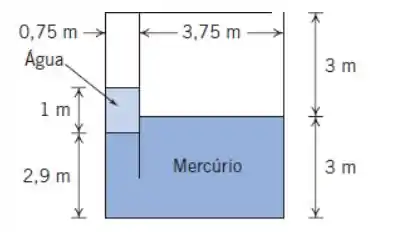
Um tanque repartido contém água e mercúrio conforme mostrado na figura. Qual é a pressão manométrica do ar preso na câmara esquerda? A que pressão deveria o ar da câmara esquerda ser comprimido de modo a levar a superfície da água para o mesmo nível da superfície livre na câmara direita?
Passo 1
Vamos lá! A gente quer achar a pressão do ar preso no lado esquerdo da câmara!
Em questões assim é sempre bom começar desenhando um esqueminha pra a gente achar os pontos que podem ser interessantes pra a gente!!
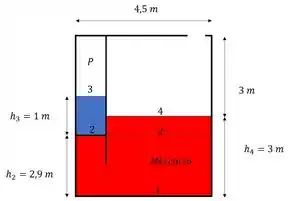
Para marcar esses pontos não precisa pensar de mais!! É só marcar todas as superfícies e interfaces e quando os lados se comunicam, como é este caso a pressão de um mesmo líquido na mesma altura tem o mesmo valor!!
Então é legal marcar um ponto ai também!
Nesse caso temos os pontos e e:
Da mesma forma o ponto tem a mesma pressão tanto do lado esquerdo quanto no lado direito!
Passo 2
Se temos , vamos começar calculando :
Como em cima de temos uma coluna de ar com a desidade suuuper pequena, podemos dizer que !
Agora vamos para
Mas:
Ficamos com:
Igualando:
Isolando :
Para, , e , podemos calcular:
Ou:
Passo 3
Queremos que a superfície da água esteja no mesmo nível que a superfície do mercúrio, ficaria assim:
Ainda podemos fazer :
Igualando e isolando o :
-
Para que existe esse nivelamento que a gente quer, temos que ter , vamos substituir na equação a cima e dar uma arrumadinha:
)
Uhuuuul!!