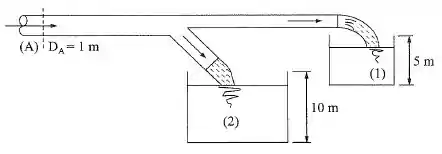
Os reservatórios da figura são cúbicos. São enchidos pelos tubos, respectivamente, em e . Determinar a velocidade da água na seção , sabendo que o diâmetro do conduto nessa seção é .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Pela equação da continuidade, sabemos que a vazão que entra deve ser igual a vazão que sai. Portanto:
Temos que:
Desenvolvendo, temos que:
Substituindo os valores, temos que:
Logo: