Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 8.Exercício - Ex. 18
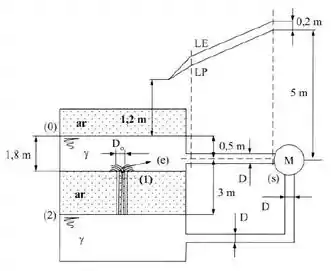
Os reservatórios do sistema não podem ser considerados de grandes dimensões; porém, deseja-se que seus níveis sejam constantes. São dados: ; ; traçado quantitativo de LE e LP entre (s) e (0) na figura; . Determinar:
a) as pressões e ;
b) a perda de carga entre (s) e (0);
c) o coeficiente de descarga do orifício ‘e’.
Passo 1
Vamos começar o exercício encontrando as pressões e , podemos encontrar essas pressões multiplicando o peso específico do fluido pela altura manométrica indicada no desenho do enunciado, então, temos:
Passo 2
Agora para encontrar a perda de carga entre os pontos 0 e (s), basta aplicar o equilíbrio de energia entre esses dois pontos, sendo assim, temos:
Sabemos as cargas dos pontos 0 e (s) através do esquema do enunciado, dessa forma, substituindo os valores conhecidos:
Passo 3
Para encontrar o coeficiente de descarga do orifício ‘e’, vamos primeiro encontrar a velocidade real do escoamento nesse ponto, que pode ser encontrada através da equação 8.8 dessa seção, sendo que nesse caso, a altura do reservatório é representada pela diferença entre as linhas de energia e piezométrica LE e LP, e por isso, obtemos a velocidade real, e não a teórica como de costume, então, temos:
Agora podemos encontrar a expressão para a vazão real nesse ponto:
Conforme apresentado nessa seção, para um orifício de bordo delgado, a vazão real do escoamento pode ser dada por:
Então nesse caso, como temos , a equação se torna:
Passo 4
Agora igualando essa última expressão a expressão encontrada anteriormente, temos:
Então, simplificando a expressão e isolando , chegamos em:
Através do desenho, podemos ver que , e o enunciado nos disse que , então, substituindo os valores conhecidos na equação anterior: