Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 8.Exercício - Ex. 14
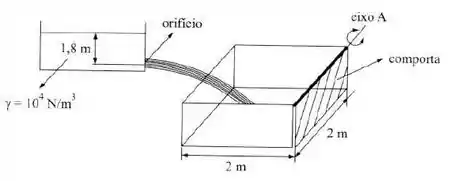
Após 5 min de funcionamento, o reservatório inferior, inicialmente vazio, está completamente cheio e, então, a comporta gira em torno do eixo A, devido ao momento de nela aplicado pela água. Determinar o coeficiente de descarga do orifício de saída do reservatório superior. Área do orifício = 0,01 m².
Passo 1
Tá legal! Quando o reservatório inferior estiver cheio, a água irá exercer uma força resultante na comporta, fazendo ela girar ao redor de A. Como temos uma comporta retangular uniforme, sabemos que a força resultante da água será aplicada a uma distância equivalente a 2/3 da altura da comporta, então, a fórmula do momento se torna:
Agora, a força que a água exerce será a pressão manométrica média multiplicada pela área total da comporta, então:
E, a pressão média exercida pela água na comporta será:
Substituindo esse valor na equação anterior, temos:
E, substituindo esse valor na expressão para o momento:
Passo 2
Agora, isolando da equação encontrada no passo 1 e substituindo os valores conhecidos, temos:
Agora podemos encontrar o volume total do reservatório inferior, que será:
E, como temos o tempo de enchimento do reservatório inferior, podemos calcular a vazão do reservatório superior (lembre-se de converter minutos para segundos)
Passo 3
Agora, podemos usar a equação 8.8 fornecida nessa seção para encontrar a velocidade teórica de saída do reservatório superior:
Com a velocidade teórica, podemos calcular a vazão teórica do reservatório superior:
E, finalmente, podemos encontrar o coeficiente de descarga: