Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 11.Problemas - Ex. 92
Resolva o Problema usando o método da efetividade .
Passo 1
Vamos lá!!
Antes de tudo recomendo ir dar uma olhadinha no problema temos aqui nos site, vai facilitar muito a compreensão dessa questão!
O problema é relativamente simples temos água escoando através do chip para dissipar calor.
Nosso problema nos pede a potência dissipada e a temperatura de saída do fluído.
Mas agora vamos ilustrar isso com nosso esqueminha pra facilitar.
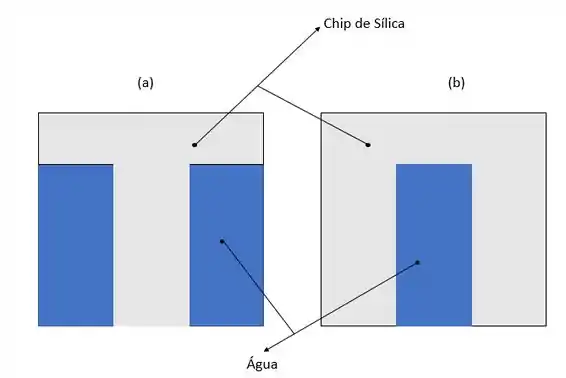
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
Vamos lá! Usaremos os para a água a .
Devido as nossas considerações podemos usar a equação para determinarmos a taxa de calor dissipado, assim temos.
Onde , e .
Da equação da eficiência temos:
Passo 3
Agora precisamos encontrar a Resistência do sistema , vamos começar avaliando o escoamento.
Sendo o diâmetro hidráulico , assim temos:
Logo nosso escoamento é laminar da tabela .
Agora calculando o nosso coeficiente convectivo.
Onde o parâmetro de canal , assim
Calculando a eficiência de canal temos:
A eficiência global de superfície é dada por:
Onde é a área do canal e é a área total do chip
Finalmente calculando nossa Resistência temos:
Para nosso da equação temos:
Substituindo na equação :
Entretanto nosso é para apenas um canal, calculando a potência dissipada por todos os canais temos:
Calculando por fim a temperatura de saída temos:
Isso é tudo pessoal! \o/
