O óleo em um motor é resfriado por ar em um trocador de calor de escoamentos cruzados no qual os dois fluidos são não misturados. Ar atmosférico entra a e . Óleo, a uma vazão de , entra a e escoa através de um tubo com de diâmetro. Supondo escoamento plenamente desenvolvido e fluxo térmico constante na parede, estime o coeficiente de transferência de calor no lado do óleo. Sendo o coeficiente global de transferência de calor por convecção igual a e a área total de transferência de calor igual a , determine a efetividade. Qual é a temperatura de saída do óleo?
Passo 1
Vamos lá!!
O problema é relativamente simples eles no pede o coeficiente de transferência de calor do óleo a temperatura de saída do óleo e a efetividade do transformador de calor.
Mas agora vamos ilustrar isso com nosso esqueminha pra facilitar.
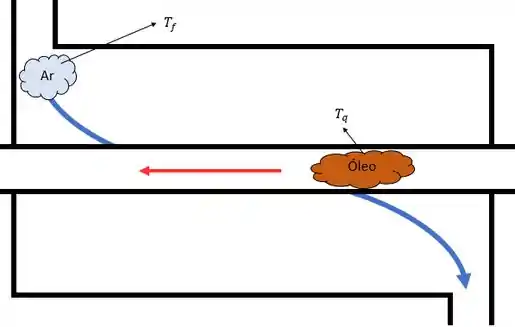
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
Vamos lá! temos que área de transferência de calor, iremos usar os dados da tabela para o óleo de motor e a tabela para a água, vamos começar calculando o coeficiente de transferência de calor do óleo:
Vamos avaliar o escoamento do óleo da equação temos:
Como nosso escoamento é laminar, seguindo as considerações e temos:
Passo 3
Agora para matar essa só precisamos calcular a eficiência do nosso trocador de calor e a temperatura de saída, do método , nós temos:
Lembrando que é nossa capacidade calorifica de cada fluído!
Para :
Por fim calculando nosso parâmetro , temos:
Agora indo na figura do livro para e , temos:
Passo 4
Finalmente encontrando a temperatura de saída do óleo usando as equações e chegaremos a seguinte equação:
Como isolando temos:
Isso é tudo pessoal! \o/
